Предметные олимпиады. 5-11 классы. Математика. Программа для установки через интернет
| Код | СИ-19г |
| Авторы-составители | Дегтярь Л.Н. и др. |
| Издательство | Учитель, 2023 |
| Серия | Задания для подготовки к олимпиадам |
| Электронная версия | скачать |
| УДК | 372.016:51*05/11 |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
Предназначено учителям математики, организаторам олимпиад.
Минимальные системные требования:
- операционная система - Windows XP/VISTA/7/8/8.1;
- процессор - Pentium-II;
- оперативная память - 256 МВ;
- разрешение экрана - 1024х768;
- свободное место на жестком диске - 400 МВ.
С этим товаром покупают
Примеры документов
Введение
Одним из основных в оценке деятельности образовательного учреждения является показатель динамики образовательных достижений. На основе выявления характера динамики образовательных достижений обучающихся можно оценивать эффективность учебного процесса, работы учителя или образовательного учреждения, системы образования в целом.
В числе наиболее адекватных инструментов оценки динамики образовательных достижений – портфель достижений ученика. Портфель достижений может быть отнесен к разряду аутентичных индивидуальных оценок, ориентированных на демонстрацию динамики образовательных достижений в широком образовательном контексте.
В числе детских работ, систематизированных материалов наблюдений в портфель достижений ученика начальной школы рекомендуется включать материалы, характеризующие достижения обучающихся в рамках внеучебной (школьной и внешкольной) и досуговой деятельности – результаты участия в олимпиадах, конкурсах, смотрах и др. Основное требование, предъявляемое к этим материалам, – отражение в них степени достижения планируемых результатов освоения Примерной образовательной программы начального общего образования*.
В пособии представлены олимпиадные задания с ответами по математике для учащихся 5–11 классов. Авторы-составители дают несколько вариантов заданий. Творчески работающий учитель может варьировать содержательную часть, самостоятельно формируя, изменяя блоки заданий, ведя подготовку обучающихся поступательно, давая возможность всем желающим попробовать свои силы в выполнении олимпиадных заданий. Общий объем заданий олимпиады подобран таким образом, чтобы выявить детей с высоким интеллектуальным потенциалом, обладающих нестандартным мышлением и способных к выдвижению новых идей. Время на выполнение заданий не регламентируется, что позволяет быть успешными также детям, которые в силу своих индивидуальных особенностей работают в медленном темпе.
В ходе проверки выполненных заданий проводится статистический анализ, позволяющий определить их сложность. С одной стороны, это дает возможность объективизировать систему оценивания. С другой стороны, статистический анализ выполнения детьми тех или иных заданий позволяет судить об эффективности школьного образования в формировании способности использовать предметные знания при решении учебно-познавательных и учебно-практических задач с привлечением средств, релевантных содержанию учебного предмета (использование знаково-символических средств; моделирование; сравнение, группировка и классификация объектов; действия анализа, синтеза, сравнения и обобщения; установление связей и аналогий; поиск, преобразование, представление и интерпретация информации, рассуждения)**.
Предназначено учителям математики для подготовки обучающихся к олимпиадам, может быть использовано в качестве дополнительного материала в урочной и внеклассной работе; рекомендовано родителям для занятий с детьми по развитию интеллектуальных, творческих способностей, расширению кругозора.
Литература
Для учителя:
1. Афонькин, С. Ю. Учимся мыслить логически: увлекательные задачи для развития логического мышления / С. Ю. Афонькин. – СПб. : Литера, 2002. – 144 c.
2. Варшавский, И. К. Текстовые задачи на едином государственном экзамене / И. К. Варшавский, М. Я. Гаиашвили, Ю. А. Глазков // Математика в школе. – 2006. – № 1. – С. 6–19.
3. Вигдорчик, Е. А. Элементарная математика в экономике и бизнесе / Е. А. Вигдорчик, Т. М. Нежданова. – М. : Вита-Пресс, 1995. – 96 с.
4. Германович, П. Ю. Сборник задач по математике на сообразительность : пособие для учителя / П. Ю. Германович. – М. : Учпедгиз, 1960. – 226 с.
5. Дорофеев, Г. В. Процентные вычисления. 10–11 классы : учеб.-метод. пособие / Г. В. Дорофеев, Е. А. Седова. – М. : Дрофа, 2003. – 144 с.
6. Жохов, В. И. Преподавание математики в 5–6 классах : метод. пособие / В. И. Жохов. – М. : Мнемозина, 2008.
7. Занимательные дидактические материалы по математике. Сборник заданий / авт.-сост. В. В. Трошин. – М. : Глобус, 2008. – 298 с.
8. Каганов, Э. Д. 400 самых интересных задач с решениями по школьному курсу математики для 6–11 классов / Э. Д. Каганов. – М. : ЮНВЕС. – 1998. – 288 с.
9. Канашева, Н. А. О решении задач на проценты / Н. А. Канашева // Математика в школе. – 1995. – № 5. – С. 24.
10. Липсиц, И. В. Экономика без тайн / И. В. Липсиц. – М. : Вита-Пресс, 1994. – 352 с.
11. Нагибин, Ф. Ф. Математическая шкатулка / Ф. Ф. Нагибин, Е. Е. Канин. – М. : Просвещение, 1984.
12. Олехник, С. Н. Старинные занимательные задачи / С. Н. Олехник, Ю. В. Нестеренко, М. К. Потапов. – М. : Дрофа, 2005. – 160 с.
13. Потапов, М. К. Конкурсные задачи по математике : справ. пособие. / М. К. Потапов, С. Н. Олехник, Ю. В. Нестеренко. – 3-е изд. – М. : Наука, 2003. – 416 с.
14. Развивающие задачи для математического досуга / сост. Э. А. Кремень, З. С. Сухотина. – М. : Школа-Пресс, 1993. – 112 с.
15. Рязановский, А. Р. Задачи на части и проценты / А. Р. Рязановский // Математика в школе. – 1992. – № 1. – С. 18.
16. Саранцев, Г. И. Упражнения в обучении математике / Г. И. Саранцев. – М. : Просвещение, 1995. – 240 с.
17. Сборник задач по математике для поступающих во втузы / авт. кол. В. К. Егерев, В. В. Зайцев, Б. А. Кордемский. – М. : Мир и Образование : Оникс-ЛИТ, 2013. – 528 с.
18. Сборник элективных курсов: математика. 8–9 классы / авт.-сост. В. Н. Студенецкая, Л. С. Сагателова. – Волгоград : Учитель, 2006. – 205 с.
19. Симонов, А. С. Проценты и банковские расчеты / А. С. Симонов // Математика в школе. – 1998. – № 4.
20. Соломатин, О. Д. Старинный способ решения задач на сплавы и смеси / О. Д. Соломатин // Математика в школе. – 1997. – № 1. – С. 12–13.
21. Ткачук, В. В. Математика – абитуриенту / В. В. Ткачук. – М. : МЦНМО, 2000. – 892 с.
22. Фарков, А. В. Математические олимпиады в школе. 5–11 класс. – 3-е изд., испр. и доп. / А. В. Фарков. – М. : Айрис-Пресс, 2004. – 176 с.
23. Чесноков, А. С. Дидактические материалы по математике для 5, 6 классов / А. С. Чесноков, К. И. Нешков. – М. : Просвещение, 2010.
24. Шевкин, А. В. Текстовые задачи по математике в 5–6 классах : книга для учителя / А. В. Шевкин. – М. : Илекса, 2011. – 108 с.
25. Шорина, С. П. Обоснование старинного способа решения задач на смеси / С. П. Шорина // Математика в школе. – 1997. – № 6. – С. 77.
26. Шуба, М. Ю. Занимательные задания в обучении математике : книга для учителя / М. Ю. Шуба. – М. : Просвещение, 1994. – 225 с.
Интернет-ресурсы.
1. Глейзер, Г. И. История математики в школе (4–6 кл.) : пособие для учителей. – М. : Просвещение, 1981. – 239 с. – Режим доступа : http://svoy.ru/book/?gclid=CNq9-KDO5LsCFcNF3godWSUAlQ
2. Колягин, Ю. М. Факультативные курсы по математике для 10–11 классов / Ю. М. Колягин, Н. Е. Федорова. – М. : НИИ школ, 1989. – 374 с. – Режим доступа : http://math-portal.ru/ izdatelstvo/42-fakultativnye-kursy-po-matematike-dlya-10-11-klassov. html
3. Лурье, М. В. Задачи на составление уравнений. 3-е изд., перераб. / М. В. Лурье, Б. И. Алексанров. – М. : Наука, 1990. – 96 с. – Режим доступа : http://www.alleng.ru/d/math/math124.htm
4. Пойа, Д. Как решать задачу : пособие для учителей. 2-е изд. / Д. Пойа. – М. : Учпедгиз, 1961. – 208 с. – Режим доступа : http://rutracker.org/forum/viewtopic.php? t=3150029
5. Шарыгин, И. Ф. Решение задач, факультативный курс по математике, 10 класс / И. Ф. Шарыгин. – М. : Просвещение, 1989. – Режим доступа : http://rutracker.org/forum/viewtopic.php?t=3135582
Для учащихся:
1. Алгебра : сб. заданий для подготовки к итоговой аттестации в 9 кл. / авт. кол. Л. В. Кузнецова [и др.]. – М. : Просвещение, 2006. – 192 с.
2. Досуг
5 класс
5 КЛАСС
I тур
(школьный уровень)
Вариант 1
Задания, оцениваемые в 5 баллов.
1. В доме 12 чашек и 9 блюдечек. Дети разбили половину чашек и 7 блюдечек. Сколько чашек осталось без блюдечек?
а) 1; б) 3; в) 5; г) 7; д) 4.
2. Кирпич весит 1 кг и еще полкирпича. Сколько весят 5 кирпичей?
а) 10; б) 3; в) 5; г) 7; д) 4.
3. На левой стороне улицы находятся дома с нечетными номерами от 1 до 19, а на правой стороне – дома с четными номерами от 2 до 14. Сколько домов на этой улице?
а) 10; б) 16; в) 12; г) 17.
4. Стали вороны садиться по одной на березу – не хватило одной березы; стали садиться по две – одна береза оказалась лишней. Сколько было ворон и сколько берез?
а) Четыре вороны, две березы;
б) две вороны, три березы;
в) три вороны, четыре березы;
г) четыре вороны, три березы.
5. Древнеегипетская задача.
Количество и его четвертая часть дают нам вместе 15. Назовите количество.
а) 8; б) 6; в) 12; г) 10.
6. В клетке сидят кролики и фазаны. Всего у них 18 ног. Узнайте, сколько в клетках тех и других. Укажите все решения.
Задания, оцениваемые в 10 баллов.
1. 6 рыбаков съели 6 судаков за 6 дней. За сколько дней 10 рыбаков съедят 10 судаков?
а) 10; б) 6; в) 12; г) 8.
2. Пользуясь только сложением, запишите число 28 при помощи пяти двоек.
3. Если бы у красного дракона было на 6 голов больше, чем у зеленого, то у них было бы 34 головы на двоих. Но у красного дракона на 6 голов меньше, чем у зеленого. Сколько голов у красного дракона?
а) 10; б) 6; в) 12; г) 8.
Задание, оцениваемое в 25 баллов.
«Задача Гаусса».
Известно, что когда 9-летнему Гауссу учитель предложил найти сумму всех натуральных чисел от 1 до 100, то Гаусс справился с этим заданием так быстро, что даже удивил своего учителя. Найдите и вы сумму чисел от 1 до 100.
Вариант 2
Задания, оцениваемые в 5 баллов.
1. Экипаж, запряженный тройкой лошадей, за 1 час проехал 15 км. С какой скоростью ехала каждая лошадь?
а) 15 км/ч; в) 45 км/ч;
б) 1 км/ч; г) 5 км/ч.
2. В коробке лежали 15 шаров: красные, белые и черные. Белых шаров в 7 раз больше, чем красных. Сколько черных шаров?
а) 1; б) 3; в) 5; г) 7; д) 9.
3. Какое число получается при сложении цифр, указанных на диске телефона?
а) 33; б) 36; в) 42; г) 45.
4. Кирпич весит 2 кг и еще полкирпича. Сколько весят 4 кирпича?
а) 18; б) 6; в) 12; г) 16.
5. Для того чтобы разрезать металлическую балку на две части, нужно уплатить за работу 5 р. Сколько будет стоить работа, если балку нужно разрезать на 10 частей?
а) 35; б) 45; в) 42; г) 40.
6. Каждый последующий набор кружочков строится из предыдущего, как это показано на рисунке. Сколько кружочков нужно добавить к следующему набору?

а) 11; б) 13; в) 15; г) 7; д) 9.
Задания, оцениваемые в 10 баллов.
1. 4 маляра окрашивают 6 комнат за 5 часов. За сколько часов 12 маляров окрасят 18 комнат?
6 класс
6 КЛАСС
I тур
(школьный уровень)
Вариант 1
Задания, оцениваемые в 5 баллов.
1. Детский сад закупил несколько ящиков свеклы по 5 кг каждый и несколько ящиков моркови по 8 кг каждый. Сколько ящиков свеклы и моркови было куплено?
2. Имеются контейнеры двух видов: по 130 кг и 160 кг. Сколько было контейнеров первого и сколько второго вида, если вместе они весят 3 тонны? Укажите все решения.
3. Полтрети – число 100. Что это за число?
а) 600; в) 300;
б) 900; г) 1200.
4. Дина, Лена, Настя живут на разных этажах. На каком этаже живет каждая девочка, если Дина не живет на втором, а Лена ни на втором, ни на третьем?
5. Цифры от 1 до 9 расставьте в кружках так, чтобы сумма цифр на каждой стороне треугольника была равна числу 20.
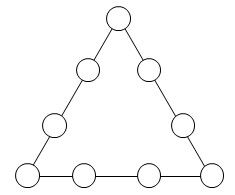
Задания, оцениваемые в 10 баллов.
1. Найдите число, если 16 % этого числа равны 10 % числа 4,8.
2. Упростите выражение: 400 · 0,008 · k · 0,025 · 9,2 · 125.
3. Среднее арифметическое трех чисел равно 3,6. Первое число равно 1,25, второе в 1,6 раза больше. Найдите третье число.
Задания, оцениваемые в 20 баллов.
1. Найдите произведение a и b, если их наименьшее общее кратное равно 420, а наибольший общий делитель равен 30.
2. Смесь сухофруктов состоит из 5 частей чернослива и 3 частей изюма. Сколько граммов чернослива в 320 г этой смеси?
Вариант 2
Задания, оцениваемые в 5 баллов.
1. У осьминога 8 ног, а у морской звезды 5. Сколько в аквариуме тех и других, если всего у них 39 ног?
2. На пост капитана команды претендовали три кандидата: Николаев, Окунев, Петров. Во время выборов за Петрова было отдано в 3 раза больше голосов, чем за Николаева, а за Окунева – в 2 раза меньше, чем за Николаева и Петрова вместе. Сколько процентов голосов было отдано за победителя?
3. 3 ученика делают 3 самолетика за 3 мин. Сколько учеников сделают 9 самолетиков за 9 мин?
а) 6; б) 9; в) 3; г) 10.
4. Беседуют трое: Белов, Чернов, Рыжов. Ни у одного цвет волос не соответствует фамилии. Какой цвет волос имеет каждый?
5. Цифры от 1 до 9 расставьте в кружках так, чтобы по любой прямой линии сумма их была равна числу 15.
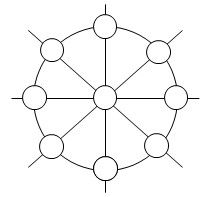
Задания, оцениваемые в 10 баллов.
1. Найдите число, если 15 % этого числа равны 20 % числа 4,5.
2. Упростите выражение: 40 · 0,125 · a · 0,25 · 0,37 · 8000.
3. Среднее арифметическое трех чисел равно 1,8. Первое число равно 1,25, второе в 1,6 раза больше. Найдите третье число.
Задания, оцениваемые в 20 баллов.
1. Найдите наименьшее общее кратное чисел m и n, если их произведение равно 4320, а наибольший общий делитель равен 12.
2. В смеси сухофруктов содержится 5 частей сушеных яблок и 3 части кураги. Сколько граммов сушеных яблок надо взять для приготовления 640 г такой смеси?
7 класс
Вариант 1
Задания, оцениваемые в 5 баллов.
1. Полторы трети километра – это сколько?
а) 1 км; б) 0,4 км; в) 0,3 км; г) 0,5 км.
2. Когда моему отцу был 31 год, мне было 8 лет, а теперь отец старше меня вдвое. Сколько мне лет теперь?
а) 32; б) 23; в) 18; г) 17.
3. Разница во времени между Москвой и Камчаткой 9 часов, а между Москвой и Прагой – 2 часа. Известно, что сейчас на Камчатке 10 часов утра, а в Москве 1 января. Какой день и какое время в Праге?
а) 31 декабря, 23 часа; в) 1 января, 2 часа;
б) 31 декабря, 24 часа; г) 1 января, 10 часов.
4. Группу школьников нужно перевезти из летнего лагеря одним из двух способов: либо двумя автобусами типа А за несколько рейсов, либо тремя автобусами типа В за несколько рейсов, причем в этом случае число рейсов каждого автобуса типа В будет на один меньше, чем рейсов каждого автобуса типа А. В каждом из случаев автобусы заполняются полностью. Какое максимальное количество школьников можно перевезти при указанных условиях, если в автобус типа В входит на 7 человек меньше, чем в автобус типа А?
Задания, оцениваемые в 15 баллов.
1. Три землекопа за 2 ч выкопали 3 ямы. Сколько ям выкопают 6 землекопов за 5 ч?
а) 30; б) 6; в) 12; г) 15.
2. Который сейчас час, если оставшаяся часть суток вдвое больше прошедшей?
а) 10 ч; б) 12 ч; в) 8 ч; г) 7 ч.
Задание, оцениваемое в 25 баллов.
Старому дедушке надо перенести с огорода в погреб 108 мешков с картофелем. Он позвал на помощь внуков. Внуки разбились на пары, и каждой паре досталось по 3 мешка. Сколько внуков у дедушки?
Вариант 2
Задания, оцениваемые в 5 баллов.
1. Мужик пошел на базар и купил лошадь за 50 р. Но вскоре он заметил, что лошади подорожали, и продал ее за 60 р. Потом он сообразил, что ехать ему не на чем, и купил ту же лошадь за 70 р. Затем он задумался, как бы не получить от жены нагоняй за такую дорогую покупку, и продал лошадь за 80 р. Сколько он заработал в результате?
а) 10 р.; б) 20 р.; в) 0 р.; г) 30 р.
2. Шарики можно разложить в пакетики, а пакетики упаковать в коробки, по 3 пакетика в одну коробку. Можно эти же шарики разложить в пакетики так, что в каждом пакетике будет на 3 шарика больше, чем раньше, но тогда в каждой коробке будет лежать по 2 пакетика, а коробок потребуется на 2 больше. Какое наибольшее количество шариков может быть при таких условиях?
Задание, оцениваемое в 10 баллов.
На кабинках колеса обозрения написаны номера: 1, 2, 3, 4… Когда кабинка с номером 25 находится в верхней точке колеса, кабинка с номером 8 находится в самой нижней точке. Сколько кабинок на колесе обозрения?
а) 18; б) 30; в) 24; г) 34.
Задания, оцениваемые в 15 баллов.
1. – Сколько тебе лет? – спросили Машу. – Я в три раза моложе папы, но и вдвое старше братишки. А братишка подбежал и пояснил, что папа старше его на 35 лет. Сколько лет каждому из них?
а) Папе 42 года, Маше 14 лет, брату 7;
б) папе 40 лет, Маше 15 лет, брату 7;
в) папе 36 лет, Маше 12 лет, брату 6;
г) папе 42 года, Маше 12 лет, брату 6.
2. Если бы завтрашний день был вчерашним, то до воскресенья осталось бы столько дней, сколько прошло от воскресенья до вчерашнего дня. Какой сегодня день?
а) Вторник; в) суббота;
б) среда; г) четверг.
Задание, оцениваемое в 25 баллов.
Жуликов, задержанных во время облавы на рынке, посадили в камеры полицейского участка. Когда их распределили по одному в каждую камеру, то одному жулику камеры не хватило. А когда посадили по двое, одна камера оказалась лишней. Сколько было жуликов и сколько камер?
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом
Отзывы
| Цитата |
|---|
| Представленные в пособии олимпиадные задания по математике с ответами для учащихся 5–11 классов помогут педагогу научить школьников использовать универсальные учебные действия; провести качественную подготовку к олимпиадам различного уровня; привить познавательный интерес к изучению учебной дисциплины и обеспечить успешное решение учебно-практических задач с учетом ФГОС. |













