Физика и астрономия. 9–11 классы. Олимпиадные задания. Программа для установки через Интернет
| Код | СИ-18ш |
| Авторы-составители | Оськина В. Т. |
| Издательство | Учитель, 2025 |
| Серия | Задания для подготовки к олимпиадам |
| Электронная версия | скачать |
| УДК | 371.3 |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
Пособие предназначено учителям физики для осуществления индивидуального и дифференцированного подхода к обучению, при работе в профильных классах с учетом ФГОС; может быть полезно обучающимся 9-11 классов для самоподготовки и самоконтроля.
Минимальные системные требования:
- операционная система - Windows XP/VISTA/7/8/8.1;
- процессор - Pentium-II;
- оперативная память - 256 МВ;
- разрешение экрана - 1024х768;
- свободное место на жестком диске - 400 МВ.
С этим товаром покупают
Примеры документов
Вариант 1
Задача 1.
Электрическим паяльником мощностью W = 500 Bт нагревают воду в кастрюле. За две минуты температура воды увеличилась от 85 Сº до 90 Сº. Затем кипятильник выключили, и за одну минуту температура воды упала на один градус. Сколько воды находится в кастрюле? Удельная теплоемкость воды равна 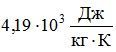 .
.
Решение
При нагревании воды расход энергии:
![]()
где t1 – время нагревания, Т2 = 90 °С, Т1 = 85 °С,
![]() – потери энергии, которые пропорциональны разности температур воды и окружающей среды и времени t.
– потери энергии, которые пропорциональны разности температур воды и окружающей среды и времени t.
При остывании воды ![]()
Так как разность температур воды и воздуха меняется незначительно, а ![]()
Так что ![]()
Отсюда 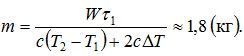
В закрытом с обоих концов цилиндре, из которого откачан воздух, подвешен на пружине скользящий без трения поршень, положение равновесия которого находится у дна цилиндра. В пространство под поршнем вводится такое количество газа, что поршень поднимается на высоту h.
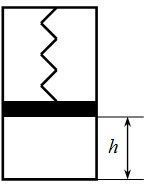
На какой высоте h1 установится поршень, если этот газ нагреть от начальной температуры T до T1? Сила, действующая со стороны пружины на поршень, пропорциональна смещению поршня.
Решение
Поршень всегда будет устанавливаться в таком положении, при котором сила давления газа равна силе сжатой пружины F = kh.
При температуре Т: 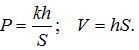
При температуре T1: 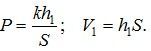
Из уравнения газового состояния получим:
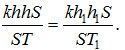
Откуда 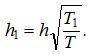
Цилиндрическая пипетка длиной L наполовину погружена в ртуть. Верхний конец ее закрывают пальцем и вынимают из ртути. Часть ртути из пипетки вытекает. Какой длины столбик ртути остался в пипетке? Атмосферное давление равно Н.
Решение
Пусть длина столбика ртути, оставшейся в пипетке, будет h.
Тогда давление воздуха в пипетке Р = Н – h, а его объем V = S(L – h).
Так как температура постоянная, то на основании закона Бойля – Мариотта Р0V0 = PV.
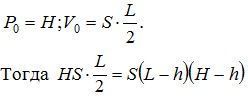
![]()
Отсюда: ![]()
Вариант 2
Задача 1.
Два автомобиля движутся с постоянными скоростями по двум взаимно перпендикулярным улицам. Скорость первого автомобиля в два раза превышает скорость второго, которая равна ![]() . В тот момент, когда второй автомобиль находился на перекрестке, первый был от него на расстоянии l = 200 м. Через какой промежуток времени после этого расстояние между автомобилями станет наименьшим?
. В тот момент, когда второй автомобиль находился на перекрестке, первый был от него на расстоянии l = 200 м. Через какой промежуток времени после этого расстояние между автомобилями станет наименьшим?
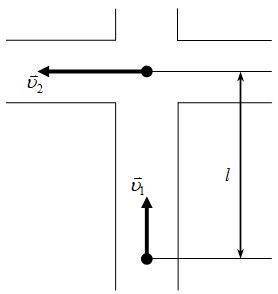
Решение
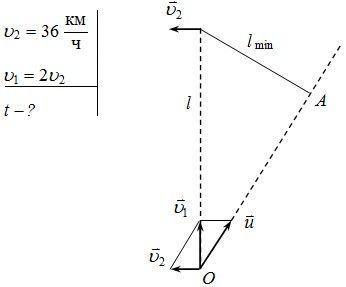
![]() , где
, где
![]() – скорость первого автомобиля относительно второго.
– скорость первого автомобиля относительно второго.

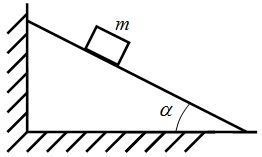
Призма находится на гладкой горизонтальной поверхности и упирается в гладкую вертикальную стену. На поверхность призмы, наклоненную под углом a к горизонту, положили брусок массой m и отпустили. Брусок стал соскальзывать, коэффициент трения бруска о поверхность призмы равен m. Найти силу давления призмы на стену.
На гладком горизонтальном столе происходит лобовой удар двух тел: одно из них массой 2m сначала покоится, а другое массой m налетает на него со скоростью u0. Найдите скорость, с которой будет двигаться после удара тело массой 2m, если известно, что в тепло при ударе переходит 20 % кинетической энергии налетающего тела.
Решение
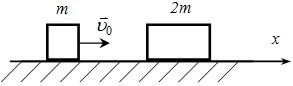
По закону сохранения импульса в проекции на х:
![]() .
.
По закону изменения энергии:
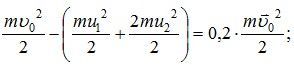
Вариант 3
Задача 1.
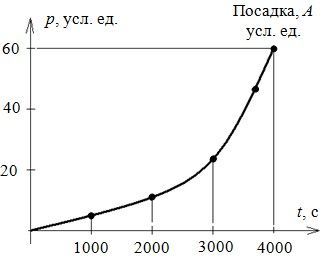
Спускаемый аппарат космического корабля опускается вертикально на поверхность планеты с постоянной скоростью, передавая на борт корабля данные о наружном давлении. График зависимости давления от времени приведен на рисунке. Оказавшись на поверхности планеты, аппарат измерил и передал на борт следующие данные: T = 700 K и g = 10 м/с2. Определить скорость спуска аппарата, если известно, что атмосфера планеты состоит из углекислого газа СО2. Найти температуру атмосферы планеты на высоте h = 15 км от ее поверхности.
Решение
Изменение давления Dr с изменением высоты Dh связано соотношением:
![]()
где r – плотность газа.
Согласно уравнению Менделеева – Клапейрона:
![]()
причем в рассматриваемой ситуации Т – температура газа именно в той точке, вблизи которой мы интересуемся изменением давления.
Так как ![]() ,
,
где u – скорость спускаемого аппарата;
Dt – время спуска,
то выражение (1) можно записать:
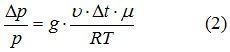
Зная соотношение ![]() , то есть тангенс угла наклона касательной в конечной точке А графика, с помощью соотношения (2) найдем скорость u.
, то есть тангенс угла наклона касательной в конечной точке А графика, с помощью соотношения (2) найдем скорость u.
Определяя из графика 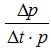 и подставляя
и подставляя ![]() для CO2, найдем, что скорость спуска аппарата космического корабля равна:
для CO2, найдем, что скорость спуска аппарата космического корабля равна:
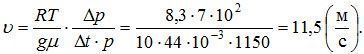
Далее, поскольку скорость аппарата ![]() , то на высоте h = 15 км над поверхностью планеты он был за 1360 секунд до посадки, то есть этому соответствует время t = 2350 c.
, то на высоте h = 15 км над поверхностью планеты он был за 1360 секунд до посадки, то есть этому соответствует время t = 2350 c.
Зная величину 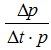 в этой точке графика, из выражения (2) найдем искомую температуру Th:
в этой точке графика, из выражения (2) найдем искомую температуру Th:
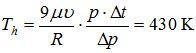 .
.
Тело массой m лежит на клине массой М с длиной наклонной плоскости l и высотой h. На какое расстояние х переместится клин за время, в течение которого тело спустится с вершины клина к его основанию, двигаясь равноускоренно? Трением пренебречь.
Решение

За время, пока тело будет соскальзывать с наклонной плоскости длиной l, оно переместится в горизонтальном направлении (то есть в направлении оси 0х) на расстояние, равное длине основания клина.
Согласно теореме Пифагора длина этого основания ![]() .
.
При этом тело двигалось равноускоренно.
Вариант 1
Задача 1.
Два одинаковых теплоизолированных цилиндрических сосуда высотой h = 75 см заполнены на одну треть: первый – водой при температуре 10 ºС, второй – льдом. Воду из первого цилиндра перелили во второй, в результате чего он заполнился на две трети объёма. По завершении теплообмена уровень заполнения его повысился на ∆h = 0,5 см. Найти начальную температуру льда tл.
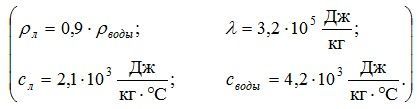
Р е ш е н и е
1. Выполнение рисунка, определение состава и температуры смеси:
1) После теплообмена объем смеси увеличился, поэтому можно считать, что либо вся вода, либо ее часть закристаллизовалась.
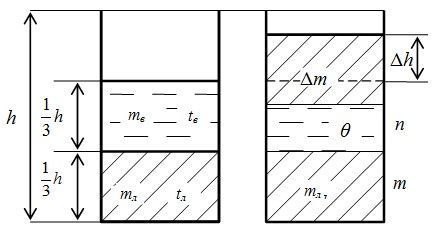
2) Определим, на сколько изменился бы уровень смеси, если бы вся вода закристаллизовалась.
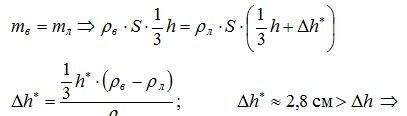
закристаллизовалась лишь часть воды, и температура смеси q равна 0 ºС.
2. Составление уравнения теплового баланса.
![]() – тепло, отданное водой.
– тепло, отданное водой.
![]() – тепло, отданное частью воды Dm при кристаллизации.
– тепло, отданное частью воды Dm при кристаллизации.
![]() – тепло, полученное льдом при нагревании до θ = 0ºС.
– тепло, полученное льдом при нагревании до θ = 0ºС.
Так как система теплоизолирована, то

3. Определение неизвестных в уравнении (1).
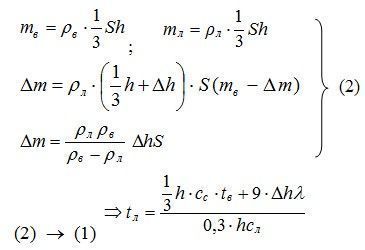
4. Расчет.
tл = –53 °С.
Лампочки Л1 и Л2, имеющие вольтамперные характеристики (графики зависимости силы тока от напряжения), показанные на рисунке, соединили последовательно и подключили к источнику с напряжением U = 12 B. Найдите силу тока, текущего при этом через лампочку Л1.
Вариант 1
Задача 1.
Звезда отстоит от полюса мира на 45°. Всегда ли ее можно видеть над горизонтом Ялты (φ = 44,5°), Санкт-Петербурга (φ = 60°), Архангельска (φ = 64,6°) и Ташкента (φ = 41,3°)?
Если речь идёт о Северном полюсе мира, то звезда будет восходящей там, где высота полюса (равная широте места) больше, чем 45°. Это Санкт-Петербург и Архангельск. Если речь идёт о Южном полюсе мира, то звезда не будет восходящей в Санкт-Петербурге и Архангельске, но появится у горизонта Ялты и Ташкента.
В полночь на небесном меридиане наблюдалось созвездие Ориона. В каком примерно созвездии находится Солнце, и в какое время года ведется наблюдение?
В это время, как видно по звёздной карте, Солнце может находиться в созвездии Стрельца (или Змееносца), а бывает это в декабре, в начале зимы.
Взрыв Тунгусского метеорита наблюдался на горизонте в городе Киренске (на реке Лене) в 350 км от взрыва. Определите, на какой высоте произошел взрыв?
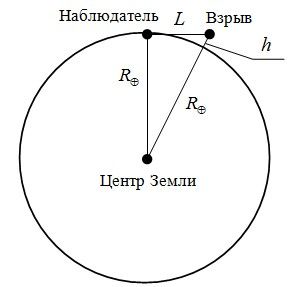
Треугольник со сторонами L, RЕ и RЕ + h – прямоугольный, поскольку взрыв был виден у горизонта, а атмосферной рефракцией мы пренебрегаем.
Следовательно, можно записать:
![]()
откуда ![]()
Поскольку радиус Земли RЕ = 6371 км и расстояние до точки взрыва L = 350 км известны, это квадратное уравнение решаем относительно высоты взрыва h.
Но можно поступить проще. Поскольку h << RЕ, можно упростить уравнение:
![]()
Следовательно,  .
.
Комета Галлея обращается вокруг Солнца за 76 лет, а планета Нептун – за 165 лет. Кто из них более удален от Солнца в точке афелия своей орбиты?
Орбита кометы сильно вытянута, поэтому в афелии она находится на расстоянии 2аk от Солнца, а планета – на расстоянии аp (а – большая полуось орбиты). Значит, отношение расстояний в афелии, найденное из третьего закона Кеплера:

Значит, комета Галлея в афелии удаляется за орбиту Нептуна.
Наблюдатель, находящийся на земном экваторе, все время видит искусственный спутник Земли у себя над головой. На каком расстоянии от земной поверхности находится этот спутник, и с какой линейной скоростью обращается он вокруг Земли?
Такой спутник называется геостационарным. Он движется к плоскости земного экватора по круговой орбите радиусом
r = R + h, где R = 6378 км – экваториальный радиус Земли,
h – высота орбиты над экватором.
Для периода обращения по круговой орбите из третьего закона Кеплера имеем:
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом













