Алгебра и начала анализа. 10 класс: поурочные планы по УМК А.Г. Мордковича и др. Программа для установки через Интернет
| Код | СИ-412.3 |
| Авторы-составители | Дюмина Т. Ю., Махонина А. А. |
| Издательство | Учитель, 2025 |
| Серия | Поурочное планирование |
| Электронная версия | скачать |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
Поурочные планы составлены по учебному комплекту:
- Мордкович, А. Г. Алгебра и начала математического анализа. 10-11 классы : в 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А. Г. Мордкович. - М. : Мнемозина, 2014;
- Задачник для учащихся общеобразовательных учреждений (базовый уровень) / А. Г. Мордкович [и др.] ; под ред. А. Г. Мордковича. - М. : Мнемозина, 2014.
Материал сгруппирован по темам.
В пособии содержатся теоретические сведения, задания для устной работы, рекомендации по объяснению нового материала, игровые формы работы, тесты, проверочные и самостоятельные работы, математические диктанты и контрольные работы.
С этим товаром покупают
Примеры документов
Урок 2 (22). Решение задач с помощью графика функции у = cos х
Урок 2 (22)
Решение задач с помощью графика
функции у = cos х
Цели: формировать умения решать графически уравнения вида cos х = f(x), строить графики кусочных функций, в записи которых встречается функция у = cos х, а также описывать функцию по её графику.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Не выполняя построения, ответьте, принадлежит ли графику функции у = cos х точка.
а) (2; 1); б) (0; 0); в) 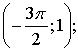
г) 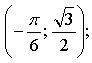 д)
д) 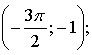 е) (–4; 1).
е) (–4; 1).
2. Задайте аналитически дугу числовой окружности.
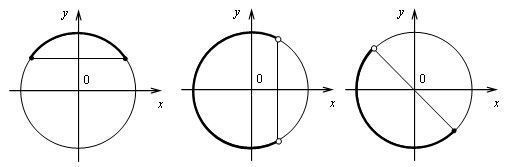
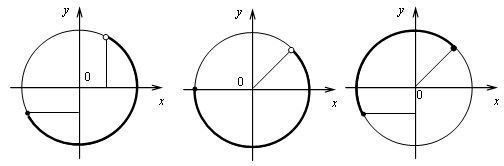
III. Формирование умений и навыков.
1. Учащиеся уже умеют решать графически уравнения вида sin х = g(x). Используем прием аналогии на данном уроке. Следует повторить алгоритм графического решения уравнения.
1-й шаг. Записать уравнение в виде cos х = f(x).
2-й шаг. В одной координатной плоскости построить графики функций у = cos х и у = f(x).
3-й шаг. Найти абсциссы точек пересечения графиков.
4-й шаг. Проверить получившиеся решения подстановкой в исходное уравнение.
2. Перед тем как приступить к решению уравнений, выполняем № 11.8 (а; б).
Решение:
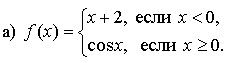
Графиком функции у = х + 2 является прямая, проходящая через точки (–4; –2), (–1; 1).
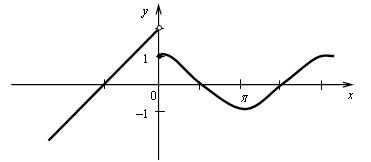
![]()
2) Общего вида.
3) На ![]() где
где ![]() – возрастает; на
– возрастает; на ![]() где
где ![]() – убывает.
– убывает.
4) Ограничена сверху.
5) унаим – не существует, унаиб – не существует.
6) Имеет разрыв в точке х = 0.
7) ![]()
б) 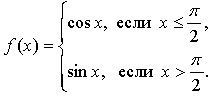

![]()
2) Общего вида.
Урок 1 (16). Формулы приведения. Мнемоническое правило запоминания
Урок 1 (16)
Формулы приведения.
Мнемоническое правило запоминания
Цели: вывести формулы приведения для углового и радианного аргумента; изучить мнемоническое правило запоминания формул; формировать умение находить значение sin tcos ttg t, ctg t при помощи формул приведения, а также значение тригонометрических выражений.
Ход урока
I. Организационный момент.
II. Проверочная работа.
Вариант 1
1. Переведите данные числа из градусной меры в радианную.
75 °; 10 °; 144 °; 1080 °.
2. Переведите данные числа из радианной меры в градусную.
![]()
3. Запишите значения синуса, косинуса и тангенса данных угловых аргументов (в виде таблицы).
0 °; 45 °; 120 °; 210 °; –90 °.
Вариант 2
1. Переведите данные числа из градусной меры в радианную.
15 °; 18 °; 108 °; 720 °.
2. Переведите данные числа из радианной меры в градусную.
![]()
3. Запишите значения синуса, косинуса и тангенса данных угловых аргументов (в виде таблицы).
30 °; 150 °; 270 °; 300 °; –30 °.
III. Объяснение нового материала.
1. Актуализация знаний.
Вычислите устно.
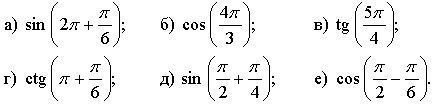
2. Решая устно указанные выше примеры, выносим на доску изученные ранее формулы.
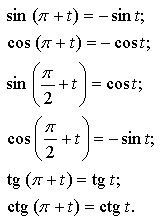
3. Показываем, что можно вывести и другие формулы приведения, где под знаком тригонометрической функции содержится выражение вида ![]()
Формулируем мнемоническое правило, которое можно записать в следующем виде:
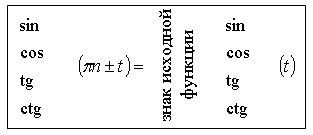
Особенное внимание обращаем на то, что выражение pn либо ![]() (кратное p или
(кратное p или ![]() ), но не
), но не ![]() и т. д.
и т. д.
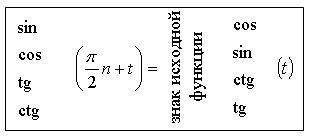
4. Рассматриваем применение формул приведения в случае аргумента, выраженного в градусах, то есть вида 90 ° + ; 180 ° – и т. д.
IV. Формирование умений и навыков.
Упражнения, решаемые на этом уроке, направлены на усвоение формул приведения. Особую сложность для учащихся представляет определение знака исходной функции. Для формирования устойчивого навыка следует использовать модели числовых окружностей с нанесенными знаками sin tcos
Урок 1 (8). Числовая окружность на координатной прямой
Урок 1 (8)
Числовая окружность
на координатной прямой
Цели: ввести понятие модели числовой окружности в декартовой и криволинейной системе координат; формировать умение находить декартовы координаты точек числовой окружности и выполнять обратное действие: зная декартовы координаты точки, определять её числовое значение на числовой окружности.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Назовите координаты точек плоскости:
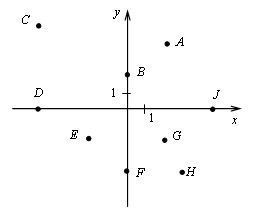
2. Назовите число, соответствующее заданной точке на числовой окружности.
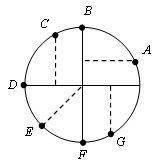
III. Объяснение нового материала.
1. Объяснение следует проводить согласно пункту учебника. Разместив числовую окружность в декартовой системе координат, следует подробно разобрать свойства точек числовой окружности, находящихся в различных координатных четвертях. Дело в том, что, изучая данную модель, учащиеся сталкиваются с определенными трудностями. Им необходимо учиться работать одновременно в двух системах координат – криволинейной и декартовой.
Для преодоления этой трудности авторы учебника применяют следующий методический прием: для точки М числовой окружности используют запись М(t), если речь идет о криволинейной координате точки М, или запись М (х; у), если речь идет о декартовых координатах точки.
2. Проводим 7-ю методическую «игру» – отыскание декартовых координат «хороших» точек числовой окружности. Речь идет о переходе от записи М(t) к М (х; у).
Можно организовать работу в парах с последующей самопроверкой (верные ответы в таблице 1 со с. 38 учебника).
3. Проводим 8-ю методическую «игру» – отыскание знаков координат «плохих» точек числовой окружности. Если, например, М(2) = М (х; у), то х < 0; у > 0. В процессе этой «игры» школьники фактически учатся определять знаки тригонометрических функций по четвертям числовой окружности.
Если класс недостаточно «сильный», то можно на этом уроке ограничиться 7-ой «игрой».
IV. Формирование умений и навыков.
1. № 5.1 (а; б), № 5.2 (а; б), № 5.3 (а; б).
Данная группа заданий направлена на формирование умения отыскивать декартовы координаты «хороших» точек на числовой окружности.
Решение:
№ 5.1 (а).
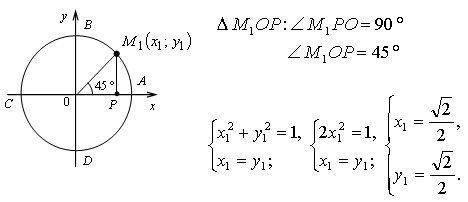
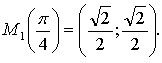
Урок 1 (26). Понятия функций y = tg x, y = ctg x
Урок 1 (26)
Понятия функций y = tg x, y = ctg x
Цели: ввести понятия функций y = tg x и y = ctg x, рассмотреть их основные свойства и построить графики; формировать умения находить значение функции y = tg x (y = ctg x) для заданных аргументов; строить графики; решать уравнения вида tg x = а и ctg x = а.
Ход урока
I. Организационный момент.
II. Проверочная работа.
Вариант 1
1. Постройте график функции ![]()
По графику найдите:
а) наименьшее и наибольшее значения функции;
б) нули функции;
в) значения аргумента, при которых функция принимает положительные значения.
2. Решите графически уравнение ![]()
Вариант 2
1. Постройте график функции ![]()
По графику найдите:
а) наименьшее и наибольшее значения функции;
б) нули функции;
в) значения аргумента, при которых функция принимает отрицательные значения.
2. Решите графически уравнение ![]()
Вариант 3
1. Постройте график функции ![]()
По графику найдите:
а) наименьшее и наибольшее значения функции;
б) нули функции;
в) значения аргумента, при которых функция принимает положительные значения.
2. Решите графически уравнение 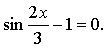
Вариант 4
1. Постройте график функции ![]()
По графику найдите:
а) наименьшее и наибольшее значения функции;
б) нули функции;
в) значения аргумента, при которых функция принимает отрицательные значения.
2. Решите графически уравнение ![]()
III. Устная работа.
Вычислите.
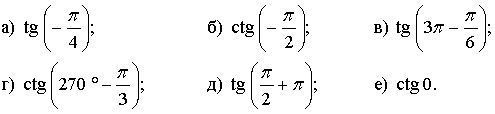
IV. Объяснение нового материала.
1. По определению 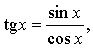 значит, функция y = tg x определена во всех точках, кроме
значит, функция y = tg x определена во всех точках, кроме ![]() (для этих значений cos х = 0). Учащиеся получают представление об области определения функции y = tg x.
(для этих значений cos х = 0). Учащиеся получают представление об области определения функции y = tg x.
2. Из формул приведения ![]() делаем вывод, что функция y = tg x – периодическая с основным периодом Т = p.
делаем вывод, что функция y = tg x – периодическая с основным периодом Т = p.
3. Из ранее известных свойств: ![]() значит, функция y = tg x – нечетная.
значит, функция y = tg x – нечетная.
4. Используя таблицу значений, либо, что удобнее, числовую окружность с линией тангенсов, выбираем контрольные точки и строим одну ветвь графика y = tg x (тангенсоиды).
Обращаем внимание учащихся, что в отличие от «похожего» графика – кубической параболы – ветвь тангенсоиды не «прижимается» в начале координат к оси 0х, а выходит как бы под углом 45 ° (биссектриса).
5. После выполнения построения графика ученики должны прочитать его и отметить оставшиеся свойства функции y = tg x:
а) Возрастает на 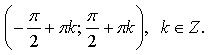
б) Не ограничена.
Урок 2 (17). Преобразование выражений с помощью формул приведения
Урок 2 (17)
Преобразование выражений
с помощью формул приведения
Цели: формировать умения преобразовывать выражения, а также решать уравнения (и неравенства) с использованием формул приведения; подготовить к контрольной работе.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Выразите в радианной мере углы, равные:
а) 90 °; б) 30 °; в) 45 °; г) 60 °;
д) 180 °; е) –18 °; ж) –360°; з) 120 °.
2. Определите знак числа.
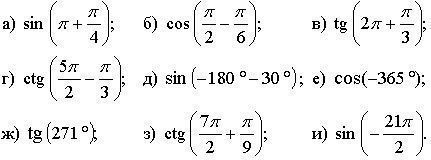
III. Формирование умений и навыков.
Все задания, выполняемые на этом уроке, можно разбить на 2 группы.
1-я группа. Преобразование тригонометрических выражений с помощью формул приведения.
2-я группа. Решение уравнений (неравенств) с помощью формул приведения.
Перед выполнением заданий повторяем мнемоническое правило и алгоритм применения формул приведения:
1-й шаг. Выражаем аргумент тригонометрической функции в виде pn + t или ![]() где
где ![]()
2-й шаг. Заменяем аргумент t, оставляя функцию при кратности pn или меняя функцию на «родственную» при кратности ![]()
3-й шаг. Ставим перед функцией знак, который имела бы исходная функция при заданном аргументе.
1-я группа.
№ 9.9 (а; б), № 9.10.
Решение:
№ 9.9.
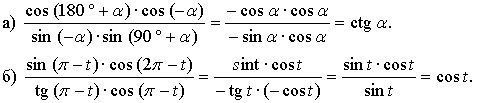
№ 9.10.
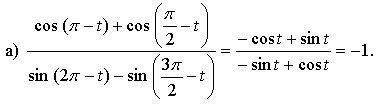
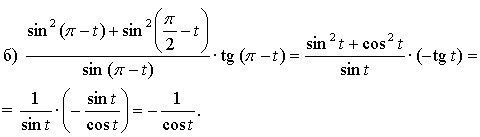
2-я группа.
№ 9.12 (а; б), № 9.13 (а), № 9.14 (а).
Решение:
№ 9.12.
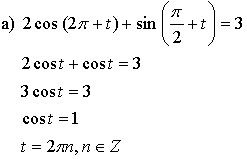
Ответ: ![]()
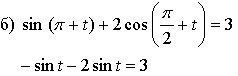
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом









