Алгебра. 7 класс: поурочные планы по учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.Б. Суворовой. Программа для установки через Интернет
| Код | СИ-351.4 |
| Авторы-составители | Дюмина Т. Ю., Махонина А. А. |
| Издательство | Учитель, 2025 |
| Серия | Поурочное планирование |
| Электронная версия | скачать |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
- Алгебра. 7 класс : учеб. для общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова ; под. ред. С. А. Теляковского. - М. : Просвещение, 2012.
Материалы, представленные на диске, систематизированы по разделам: "Выражения, тождества, уравнения", "Функции", "Степень с натуральным показателем", "Многочлены", "Формулы сокращенного умножения", "Системы линейных уравнений".
Предлагаемые разработки уроков содержат задания для устной работы, рекомендации к объяснению нового материала, тесты, проверочные и самостоятельные работы, математические диктанты и др.
Целью данного электронного пособия является практическая помощь учителю математики в выборе путей построения урока, отвечающего современным требованиям дидактики и практической педагогики.
С этим товаром покупают
Примеры документов
Урок 1. Числовые выражения, порядок действий в них, использование скобок
Урок 1
Числовые выражения, порядок действий в них,
использование скобок
Цели: ввести понятия числового выражения, значения числового выражения; формировать умение находить значение числового выражения, выполняя действия над числами и используя скобки.
Ход урока
I. Устная работа.
Вычислите.
а) 13 – 18,5; б) –19 + 21,3; в) –14 – 71,03;
г) 17 – (–21,3); д) – (–3 – 2,8); е) 3 · 15 – 7;
ж) 12 – 16 : 4; з) (15 – 2) · (–3); и) (–2) ∙ ![]() ; к) 7 :
; к) 7 : ![]() .
.
II. Объяснение нового материала.
1. Для введения понятия «числовое выражение» целесообразно сообщить учащимся следующую информацию. При решении многих задач приходится над заданными числами производить арифметические действия: сложение, вычитание, умножение и деление. Но часто, прежде чем доводить до конца каждое из этих действий, удобно заранее указать порядок (план), следуя которому надо производить эти действия. Этот план сводится к тому, что по данным задачи с помощью чисел, знаков действий и скобок составляется числовое выражение.
2. Разбираем задачу со с. 5 учебника и показываем на примере полученное числовое выражение.
следует привести достаточное число различных числовых выражений:
43 : 5; 9,6 – 3 · 1,2; 5 · (7,4 – 6,1);
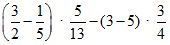 ; (39 – 15) : 23 +
; (39 – 15) : 23 + 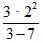 .
.
3. Если в числовом выражении выполнить все указанные в нем действия, то в результате получим действительное число, про которое говорят, что оно равно данному числовому выражению и называется значением выражения.
Подчеркнем, что числовое выражение дает указание, какие арифметические действия и в каком порядке мы должны произвести над данными числами. Скобки помогают установить порядок действий.
Задание. расставить над знаками арифметических действий порядковые номера их выполнения.
3,5 – 8 · 2,7 + 2,5 : 3 – 112 · 5;
(3,5 – 8) · 2,7 + 2,5 : (3 – 112) · 5;
3,5 – 8 · (2,7 + 2,5 : 3) – 112 · 5;
3,5 – 8 · (2,7 + 2,5 : (3 – 112)) · 5.
4. № 1 (а, г, ж).
Решение:
а) 6,965 + 23,3 = 30, 265;
г) 6,5 · 1,22 = 7,93;
ж) 53,4 : 15 = 3,56.
5. Мы, конечно, предполагаем, что все действия возможно осуществить. Поясним эти слова. Всегда возможно произвести сложение, вычитание и умножение любых чисел. А вот делить числа одно на другое возможно, только если делитель не равен нулю: на нуль делить нельзя. Если в данном выражении на некотором его этапе требуется делить на нуль, то это требование неосуществимо. Такое выражение не имеет смысла.
Например, выражения 35 : (4 · 2 – 8) и 0,37 – 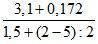 не имеют смысла, потому что при выполнении указанных в них действий появляется необходимость делить на нуль.
не имеют смысла, потому что при выполнении указанных в них действий появляется необходимость делить на нуль.
6. Замечаем, что числовое выражение может состоять и из одного числа.
III. Формирование умений и навыков.
Все упражнения, выполняемые на этом уроке, можно разбить на группы:
1-я группа. Нахождение значения числового выражения, представляющего собой сумму или разность, произведение или частное.
2-я группа. Нахождение значения числового выражения, содержащего в записи два и более арифметических действия, а также скобки.
3-я группа. Задания на составление числовых выражений, отвечающих заданным условиям (наличие или отсутствие смысла, равенство определенному значению).
1-я группа
1. № 1 (б; д; з). Самостоятельно.
2. Найдите сумму или разность.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() ;
;
ж) ![]() ; з)
; з) ![]() ; и)
; и) ![]() .
.
Урок 2. Решение задач по теме "Числовые выражения"
Урок 2
Решение задач по теме
«Числовые выражения»
Цели: продолжить формировать умение находить значение числового выражения; формировать умение составлять числовое выражение по условию задачи и находить его значение.
Ход урока
I. Устная работа.
1. Найдите значение числового выражения.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) 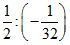 ;
;
д) –0,3 · (–0,2); е) –3,7 – 2,3; ж) –8,1 : (–9); з) –3,4 + 7,5.
2. Найдите:
а) 10 % от 480; г) 25 % от 36;
б) 1 % от 500; д) 2 % от 150;
в) 50 % от 23; е) 20 % от 45.
II. Проверочная работа.
Вариант 1
1. Вычислите.
а) ![]() ; б)
; б) 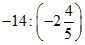 .
.
2. Найдите значение выражения.
0,7 · 1,3 + 5,1 : 0,17.
Вариант 2
1. Вычислите.
а) 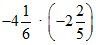 ; б)
; б) 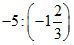 .
.
2. Найдите значение выражения.
1,8 · 0,4 + 6,4 : 0,16.
III. Актуализация знаний.
На этом уроке учащиеся составляют числовое выражение по условию задачи на проценты, на работу, на движение. Следует повторить понятия «процент», нахождение процента от числа и числа по его проценту.
1. № 7 (в; г).
2. Найдите число, если 17 % его равны:
а) 340; б) 2,89.
3. Сколько процентов число 8 составляет от числа:
а) 16; б) 0,8?
4. Выразите десятичной дробью числа его процент:
а) 43 %; б) 11,4 %.
5. Выразите в процентах дробь числа:
а) 0,5; б) 1,35.
IV. Формирование умений и навыков.
При решении упражнений следует обращать внимание учащихся на обоснование получаемого числового выражения, а также на грамотную запись.
1. № 8.
Решение:
Для нахождения количества жира в молоке необходимо найти 3,2 % от числа 200. Выразим 3,2 % обыкновенной или десятичной дробью:
3,2 % = ![]() = 0,032.
= 0,032.
Умножим данное число на дробь и получим числовое выражение: 0,032 · 200. Найдем значение данного выражения, оно равно 6,4.
Аналогично находим количество белка и углеводов:
2,5 % = ![]() = 0,025; 0,025 · 200 = 5.
= 0,025; 0,025 · 200 = 5.
4,7 % = ![]() = 0,047; 0,047 · 200 = 9,4.
= 0,047; 0,047 · 200 = 9,4.
Ответ: 6,4 г; 5 г; 9,4 г.
2. Завод по плану должен был изготовить 537 000 изделий. План был выполнен на 102,5 %. Установите:
а) сколько изделий выпустил завод;
б) сколько изделий выпустил завод сверх плана.
Решение:
а) Выразим 102,5 % обыкновенной или десятичной дробью:
102,5 % = ![]() = 1,025 =
= 1,025 = ![]() .
.
Умножим данное число на дробь и найдем значение выражения.
537 000 ∙ ![]() = 537 ∙ 1025 = 550 425.
= 537 ∙ 1025 = 550 425.
б) По плану завод должен был изготовить 537 000, а изготовил 550 425 изделий, значит, сверх плана он изготовил:
550 425 – 537 000 = 13 425.
Урок 4. Решение задач по теме "Выражения с переменными"
Урок 4
Решение задач по теме
«Выражения с переменными»
Цели: продолжить формировать умение находить значение выражения с переменными; формировать умение составлять выражение с переменными по условию задачи, в том числе формулы, и находить их значение.
Ход урока
I. Устная работа.
1. Назовите выражения, не имеющие смысла.
а) 2 · 4 – 8; б) 3 · 2 : (6 – 1,5 · 4); в) 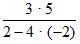 ;
;
г) 3 : 3 – 7 · 2; д) 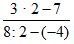 ; е)
; е) 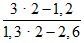 ;
;
ж) 2 : 4 – 2; з) 3 : 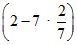 .
.
2. Найдите значение выражения 3а – b, если:
а) а = 2 и b = –4; б) а = 0 и b = ![]() ;
;
в) а = –4 и b = 5; г) а = –![]() и b =
и b = ![]() .
.
3. Сколько процентов составляет:
а) 50 от 200; б) 13 от 260;
в) 1,5 от 20; г) 240 от 80?
II. Объяснение нового материала.
На этом уроке учащиеся по аналогии с числовым выражением формулируют понятие выражения с переменной, не имеющего смысла. Затем вводится понятие формулы. Следует привести примеры различных формул, применяемых на практике (вычисление площадей, объемов, числовые формулы и т. п.). Также следует объяснить учащимся, что есть стабильные формулы, которые уже выведены и могут использоваться для расчетов. А есть задачи, для решения которых необходимо самостоятельно выявить закономерности (зависимости), описанные в условии, ввести переменные, составить выражение с переменными (формулу) и использовать его для вычисления искомого задачи при конкретных исходных данных.
III. Формирование умений и навыков.
Упражнения, решаемые на этом уроке, можно разбить на две группы:
1-я группа. Задачи практического характера, для решения которых необходимо составить формулу и вычислить по ней результат.
2-я группа. Задания на формирование грамотной математической речи (использование терминов «сумма», «разность», «произведение» и «частное») при чтении и записи выражений с переменными.
1-я группа
1. № 29.
Решение:
Если площадь первого участка а га, а с каждого га собрали 32 ц пшеницы, то со всего участка собрали 32а ц пшеницы. Аналогично получаем для второго участка урожай 40b ц пшеницы. Тогда с обоих участков был собран урожай 32а + 40b (ц). Если а = 120 и b = 80, то 32а + + 40b = 32 · 120 + 40 · 80 = 3840 + 3200 = 7040.
Ответ: 32а + 40b (ц); 7040 ц.
2. № 31.
Решение:
Фигура состоит из отдельных частей. её площадь можно найти двумя способами:
1-й способ. «Разбить» фигуру на отдельные фигуры, для которых можно легко найти площадь, и, сложив полученные результаты, получить общую площадь.
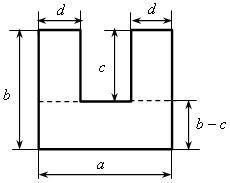
Площадь состоит из суммы площадей трех прямоугольников со сторонами: d и с; d и с; а и b – с. Их площади соответственно равны: сd; сd; а (b – с). Значит, площадь искомой фигуры составляет:
сd + сd + а (b – с) или 2сd + а (b – с).
2-й способ. Представить фигуру в виде прямоугольника со сторонами а и b с «вырезанным» прямоугольником со сторонами с и а – 2d. Их площади соответственно равны аb и с (а – 2d). Значит, площадь искомой фигуры составляет аb – с (а – 2d).
Урок 6. Решение задач по теме "Сравнение значений выражений"
Урок 6
Решение задач по теме
«Сравнение значений выражений»
Цели: продолжить формировать умение сравнивать значения числовых выражений, а также выражений с переменными при заданных значениях входящих в них переменных; ввести понятие строгого и нестрогого неравенства; формировать умение составлять выражения по условию задачи и сравнивать их значения.
Ход урока
I. Устная работа.
1. Сколько процентов составляет: а) число 8 от числа 200; б) число 15 от числа 1500; в) число 24 от числа 12; г) число ![]() от
от ![]() ?
?
2. Замените звездочку знаком: >, < или =.
а) ![]() * 3; г) 32,5 – 12 * 4,01;
* 3; г) 32,5 – 12 * 4,01;
б) ![]() * 5 – 2,5; д) (5 – 2) · 7,5 * 5 – 2 · 7,5;
* 5 – 2,5; д) (5 – 2) · 7,5 * 5 – 2 · 7,5;
в) (–2) ∙ ![]() ∙ 7 * – 3,5; е) –3,7 – 2,4 * –6,2.
∙ 7 * – 3,5; е) –3,7 – 2,4 * –6,2.
3. Прочитайте неравенство:
а) 3,7 < 3,8 < 3,95; в) –b < –a < – c;
б) k < p < 2k; г) ![]() .
.
II. Проверочная работа.
Вариант 1
1. Сравните значения выражений:
1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;
2) 2a – 3b и 3a – 2b при а = –2 и b = 3.
2. Запишите в виде двойного неравенства: t положительно и меньше 45.
Вариант 2
1. Сравните значения выражений:
1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;
2) 3a + 2b и 2a – 3b при а = –2 и b = 4.
2. Запишите в виде двойного неравенства: р отрицательно и больше –18.
III. Объяснение нового материала.
Вводится понятие строгого и нестрогого неравенства на конкретных примерах (число дней в месяце, количество пассажиров в автобусе, предельные температуры и т. п.).
Определение. Неравенства, составленные с помощью знаков > и <, называют строгими неравенствами, а неравенства, составленные с помощью знаков ≥ и ≤, называют нестрогими.
Необходимо подчеркнуть, что нестрогое неравенство является верным, если выполняется хотя бы одно соотношение:
18 ≥ 14 – верно (выполняется 18 > 14);
–35 ≤ –35 – верно (выполняется –35 = –35).
Если не выполняется ни одно из соотношений, то неравенство является неверным:
–35 ≥ –34.
Двойные неравенства также могут быть записаны с помощью знаков ≥ и ≤:
18 ≤ х ≤ 19; 1,7 < п ≤ 1,8; ![]() .
.
IV. Формирование умений и навыков.
Все упражнения, выполняемые на этом уроке, можно условно разделить на две группы:
1-я группа. упражнения на запись и чтение строгих и нестрогих неравенств.
2-я группа. решение практических задач на составление выражений и их сравнение.
1-я группа
1. № 60 (устно); № 61 (устно).
2. Задание по вариантам.
Запишите каждое предложение с помощью знаков неравенства. Подберите три значения переменной, при которых данное неравенство верно, и три, при которых неверно.
Вариант 1
1) а) t меньше 5;
б) р больше или равно –11,3;
в) т – неотрицательное число;
2) а) х меньше 5 и больше или равно 4;
б) а больше 0,01 и меньше 0,02;
в) с больше или равно –0,7 и отрицательно.
Вариант 2
Урок 8. Решение задач по теме "Свойства действий над числами"
Урок 8
Решение задач по теме
«Свойства действий над числами»
Цель: продолжить формирование умений применять основные свойства действий над числами (переместительное, сочетательное, распределительное) при нахождении значений числовых выражений.
Ход урока
I. Устная работа.
1. Вычислите:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() ;
;
ж) ![]() ; з)
; з) ![]() .
.
2. Вычислите:
а) ![]() ∙ 2; б)
∙ 2; б) ![]() : 3; в)
: 3; в) ![]() ; г) 5 :
; г) 5 : ![]() ;
;
д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
II. Актуализация знаний.
Вычислить значение каждого выражения наиболее простым способом, проговорив при этом используемое свойство действий над числами:
а) 405 · 82 + 405 · 18;
б) 707 · 13 + х · 13 при х = 293;
в) 417р – 217 · 163 при р = 163;
г) 24а – 48 · 15 при а = 33;
д) (64 · 37 + 64 · 23) : 5.
III. Формирование умений и навыков.
На этом уроке решаются задания более высокого уровня сложности.
1. № 79.
Решение:
а) 24 · 17 + 17 · 6 = 17 · (24 + 6) = 17 · 30 = 17 · 6 · 5, значит, выражение делится на 5.
б) 34 · 85 + 34 · 36 = 34 · (85 + 36) = 34 · 121 = 34 · 11 · 11, значит, выражение делится на 11.
2. № 223.
Решение:
а) 5,9 · 2,6 + 5,9 · 3,2 + 5,8 · 4,1 = 5,9 (2,6 + 3,2) + 5,8 · 4,1 = 5,9 · 5,8 +
+ 5,8 · 4,1 = 5,8 (5,9 + 4,1) = 5,8 · 10 = 58;
б) 6,8 · 8,4 – 1,6 · 8,4 + 5,2 · 1,6 = 8,4 (6,8 – 1,6) + 5,2 · 1,6 = 8,4 · 5,2 +
+ 5,2 · 1,6 = 5,2 (8,4 + 1,6) = 5,2 · 10 = 52.
3. Вычислите наиболее рациональным способом.
а) ![]() ; б)
; б) ![]() .
.
Решение:
а) Выполняем сперва умножение первой дроби на вторую, затем полученный результат – на третью дробь и т. д. Получим ![]() .
.
б) 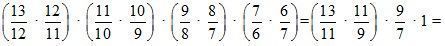
![]() .
.
4. Найдите последовательно значение каждой из разностей:
![]() , а затем значение суммы
, а затем значение суммы ![]() .
.
Решение:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
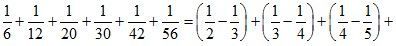
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом









