Алгебра. 7-9 классы: поурочные планы по учебникам А. Г. Мордковича, П. В. Семенова. Программа для установки через Интернет
| Код | СИ-170.5 |
| Авторы-составители | Афанасьева Т. Л., Ким Е. А., Купорова Т. И., Тапилина Л. А. |
| Издательство | Учитель, 2025 |
| Серия | Поурочное планирование |
| Электронная версия | скачать |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
На диске содержатся основные теоретические сведения, необходимые для организации современного урока дидактический материал (карточки для устного опроса, таблицы, задания творческого характера), а также контрольные работы. Поурочные планы снабжены достаточно большим количеством индивидуальных и тестовых заданий. Даны методические рекомендации по изучению отдельных тем. Подбор задач призван обеспечить высокий темп урока.
Разнообразный и полезный методический и дидактический материал позволит учителю построить урок с учетом новых технологий и современных требований, совершенствовать практические навыки и умения учащихся, формировать УУД.
Предлагаемое распределение материалов по урокам носит примерный характер. Учитель может по своему усмотрению вносить коррективы в ход урока, учитывая специфику и уровень подготовки класса.
С этим товаром покупают
Примеры документов
Линейная функция и ее график
Линейная функция и ее график
Цель: ознакомить учащихся с линейной функцией и ее графиком. Выработать у учащихся умение строить и читать график функции y = kx + b.
I. Изучение нового материала.
1. Повторить алгоритм построения графика уравнения ax + by + c = 0.
2. Помочь учащимся увидеть, что если это уравнение преобразовать к виду ![]() , а введя обозначения
, а введя обозначения ![]() ,
, ![]() , – к виду y = kx + m, то найти координаты точек соответствующей прямой удается легче и быстрее.
, – к виду y = kx + m, то найти координаты точек соответствующей прямой удается легче и быстрее.
3. Изучить определение линейной функции.
4. Познакомить учащихся с понятиями независимая переменная и зависимая переменная.
5. Выяснить с учащимися, что является графиком линейной функции.
6. Разобрать пример 1, c. 44.
7. Разобрать три математические ситуации, приведенные в учебнике, и сделать вывод, что во многих случаях недостаточно составить математическую модель ситуации, необходимо еще очертить границы применимости модели.
8. Разобрать пример 2 из учебника и подробно оформить его решение в тетрадях.
9. Разобрать и оформить решение примера 3.
10. Ввести понятия наибольшее значение функции и наименьшее значение функции.
11. Разобрать пример 4 из учебника.
12. Разобрать пример 5 и ввести понятия и условия возрастания и убывания функции.
II. Закрепление изученного материала.
На первом уроке:
Устно: № 8.1; 8.2; 8.9; 8.14 (в, г).
Письменно: № 8.15; 8.19.
На втором уроке:
Устно: № 8.4; 8.27.
Письменно: № 8.29; 8.32; 8.48; 8.52.
На третьем уроке:
Устная работа.
1. Является ли линейной функция, заданная формулой:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ?
?
Для этих формул укажите коэффициенты k и b.
2. Найдите координаты точки пересечения графика функции, заданной формулой y = 7x – 14, с: а) осью х; б) осью у.
Устно: № 8.62; 8.63.
Письменно: № 8.46; 8.50; 8.54; 8.57; 8.58; 8.61.
III. Задание на дом: § 8.
Урок 1: № 8.10; 8.14 (а, б); 8.17; 8.18.
Урок 2: № 8.28; 8.34; 8.47.
Урок 3: № 8.45; 8.53; 8.56; 8.60.
Основные понятия
Основные понятия
Цель: сформировать представление о математической модели система уравнений. Изучить графический метод решения систем уравнений.
I. Актуализация опорных знаний учащихся.
Повторить с учащимися:
1) Понятие линейного уравнения с двумя переменными.
2) Привести примеры линейных уравнений с двумя переменными.
3) Что называют решением линейного уравнения с двумя переменными.
4) Является ли решением уравнения 2x – y = 3 пара чисел:
а) (0; – 3); б) (– 1; 1);
в) (4; 5); г) (1,5; 0).
5) Что является графиком линейного уравнения с двумя переменными, сколько решений может иметь уравнение ax + by + c = 0?
II. Изучение нового материала.
1. Сформировать у учащихся представление о математической модели система уравнений.
2. Познакомить учащихся с формой записи систем уравнений.
3. Изучить, что называют решением системы уравнений.
4. Изучить графический метод решения системы линейных уравнений, разобрать и оформить решения примеров 1, 2 и 3 из учебника.
5. Обобщить результаты решений этих примеров и сделать выводы о графическом методе решения систем уравнений:
а) что собой представляют графики обоих уравнений системы?
б) в каком случае система имеет единственное решение?
в) какая система является несовместимой?
г) о какой системе говорят, что она несовместима?
6. Подвести учащихся к пониманию того, что графический метод не всегда надежен и удобен, а значит, необходим алгебраический метод решения систем.
III. Закрепление изученного материала.
На первом уроке:
Устно: № 11.1; 11.2.
Самостоятельно № 11.3; 11.4; 11.6; 11.12; 11.13.
На втором уроке:
Устная работа.
1. При каком значении с график уравнения y = 3x + c проходит через точку:
А (– 4; 0); В (0;0); М (– 3; 1); К (0; – 8)?
2. Каково взаимное расположение на координатной плоскости графиков линейных функций:
а) y = –3x + 1 и y = 5x + 2;
б) y = 6x – 5 и y = 6x + 7?
Ответ обоснуйте.
3. Устно: № 11.8; 11.9.
Письменно: № 11.16; 11.17; 11.18; 11.20; 11.21.
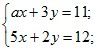
Так как первое уравнение обращается в верное равенство при х = 5 и у = –3, можно найти значение а из соотношения ![]() .
.
Теперь можем решить систему уравнений.
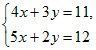
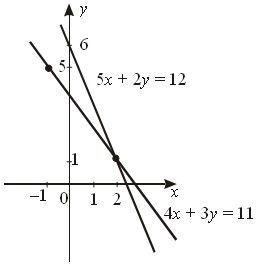
Ответ: (2; 1).
IV. Задание на дом: § 11.
Урок 1: № 11.7; 11.10.
Урок 2: № 11.15; 11.19.
Метод подстановки
Метод подстановки
Цель: сформировать у учащихся умение решать системы двух линейных уравнений методом подстановки. Обеспечить овладение всех учащихся основными алгоритмическими приемами этого метода.
I. Изучение нового материала.
1. Повторить этапы графического метода решения систем уравнений.
2. Вспомнить, какие выводы были сделаны на предыдущих уроках по этому методу.
3. Показать учащимся алгебраический метод решения примера 2 из предыдущего параграфа.
4. Изучить алгоритм решения системы двух уравнений с двумя переменными методом подстановки.
5. Разобрать и оформить в тетрадях решение примеров 1 и 2 из учебника.
II. Закрепление изученного материала.
На первом уроке:
Устная работа.
1. Является ли решением системы 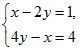 пара чисел:
пара чисел:
а) (– 1; 1); б) (2; –1); в) (6; 2,5)?
2. Приведите пример уравнения с переменными х и у, равносильного линейному уравнению:
а) x – y = 3; б) ![]() ; в)
; в) ![]() .
.
3. Назовите три решения уравнения:
а) y = 2x + 5; б) xy = 0; в) x – y = 1;
г) ![]() ; д)
; д) ![]() .
.
4. № 12.5.
Письменная работа № 12.8 (в).
в) 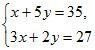
1) Из первого уравнения x = 35 – 5y;
2) Подставим найденное выражение вместо х во второе уравнение системы и решим его:
![]()
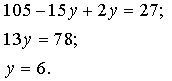
3) ![]() ;
;
x = 5.
Ответ: (5; 6).
Письменная работа № 12.9.
№ 12.9 (в, г).
На втором уроке:
I. Устная работа.
1. Решить систему уравнений
а) 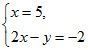
б) 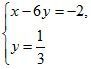
в) 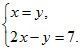
2. Пересекает ли ось х график уравнения:
а) 7x – 9y = 1; б) y – x2 = 9;
в) 3x – 0y = 5; г) 1,5y + 0x = 6;
д) 4x – y = 0?
3. № 12.6.
Письменно: № 12.14 (в, г); 12.15 (б, в, г); 12.16 (в, г).
Провести обучающую самостоятельную работу на III варианта по степени сложности.
I в а р и а н т
1. Выразите у через х:
а) x + y = 2; б) y – 6x = 1;
в) x – y = 4; г) 2y – x = 3.
2. Выразите х через у:
а) x + y = 6; б) x – 2y = 4;
в) 2y – x = 1; г) 3x – y = 2.
3. Выразите одну какую-либо переменную через другую:
а) x – 2y = 3;
б) 3x + y = 5;
в) 2y – x = 10.
4. Закончите решение системы:
Метод алгебраического сложения
Метод алгебраического сложения
Цель: обеспечить овладение основными алгоритмическими приемами решения системы двух линейных уравнений с двумя переменными методом алгебраического сложения.
У р о к 1
I. Анализ результатов самостоятельной работы.
II. Изучение нового материала.
Рассмотрев примеры 1 и 2 из учебника, изучить с учащимися приемы решения системы уравнений методом алгебраического сложения.
III. Закрепление изученного материала.
Устная работа.
1. Решите уравнение:
а) ![]() ; б)
; б) ![]() ;
;
в) 0,3y = –6; г) ![]() .
.
2. Решите систему уравнений:
а) 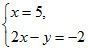 б)
б) 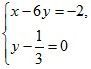
в) 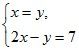
3. Пара чисел является решением уравнения x – 3y = 7. Найдите неизвестное число в паре: (…, 6); (0, …); (– 5; …); (…, 0).
Письменно № 13.2 (в, г); 13.4; 13.5 (б, г).
б) 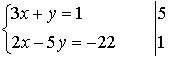
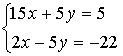
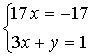
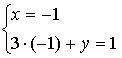
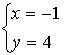
Ответ: (– 1; 4).
У р о к 2
I. Устная работа.
1. Назовите три решения уравнения:
а) y = x + 5; б) xy = 6;
в) x + y = 1; г) 6 + 0x = 2y.
2. Разложите на множители:
а) y12 = 64; б) 25a4p4 – 1;
в) 1,21 – 2,25b6; г) 4a2 + 12a + 9;
д) b4 + 10b2 + 25; е) 3,5x6 – 3,5.
3. Являются ли системы двух уравнений с двумя переменными
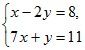 и
и 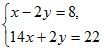 равносильными?
равносильными?
Как получить вторую систему из первой?
II. Письменно № 13.7 (в, г); 13.9 (в, г); 13.14 (в, г).
III. Самостоятельная работа.
I в а р и а н т
1. Умножьте одно из уравнений системы или каждое из них на какое-либо число так, чтобы с помощью сложения можно было исключить одну из переменных:
а) 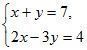 б)
б) 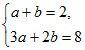
в) 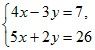
2. Закончите решение системы:
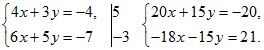
3. Решите систему уравнений:
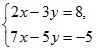
Для этого:
1) умножьте все члены первого уравнения на 5, а второго – на –3;
2) сложите почленно левые и правые части уравнения;
3) найдите х из получившегося уравнения;
Системы двух линейных уравнений с двумя переменными как матаматические модели реальных ситуаций
Системы двух линейных уравнений
с двумя переменными как математические
модели реальных ситуаций
Цель: познакомить учащихся с применением систем линейных уравнений при решении задач. Обеспечить овладение основными алгоритмическими приемами применения систем двух линейных уравнений при решении задач.
На первом уроке:
I. Устная работа.
1. Составьте уравнение, зная что:
а) длина прямоугольника х м, ширина у м, а периметр 24 м;
б) основание равнобедренного треугольника а см, боковая сторона b см, периметр 59 см;
в) туристы 5 ч ехали на автобусе со скоростью х км/ч и 8 ч на поезде со скоростью у км/ч. За эти 13 ч туристы проехали 680 км.
2. Приведите пример уравнения с переменными х и у:
а) имеющего одно решение;
б) не имеющего решений;
в) имеющего бесконечное множество решений;
г) решением которого была бы любая пара чисел.
II. Письменно: № 14.2; 14.4; 14.5.
На втором уроке:
I. Устная работа.
1. Составьте уравнение по следующему условию задачи:
а) В одном магазине было х кг яблок, а в другом у кг. За день продали: первый магазин 12 % имеющихся там яблок, а второй – 15 %, всего было продано 1,5 т яблок;
б) Тетрадь стоит х рублей, блокнот – у рублей. Два блокнота втрое дороже пяти тетрадей.
2. Разложите на множители:
а) x2 – 4y2; б) 8p3 + 1;
в) 16x4 – x6; г) 0,01 – a4;
д) ![]() ; е) –144 + p2.
; е) –144 + p2.
II. Письменно: № 14.9; 14.20.
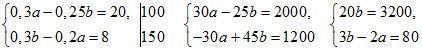
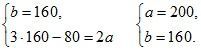
Ответ: 200; 160.
№ 14.21; 14.22; 14.24.
На третьем уроке:
I. Устная работа.
1. Составьте уравнение по условию задачи:
а) Собственная скорость катера а км/ч, скорость течения реки х км/ч. За 3 ч вверх по реке катер прошел 54 км.
б) В одной коробке х кг печенья, в другой – у кг. Если из одной коробке переложить в другую 3 кг, печенья в коробке станет поровну.
2. Представить в виде многочлена стандартного вида:
а) x (x + 3); б) (3 – a)(a + 3);
в) (x2 + 1)(1 – x2); г) (x + 1)(x2 – x + 1);
д) (1 – 2b)2; е) 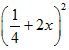 .
.
II. Письменно: № 14.27.
Пусть х см/с – скорость точки, движущейся быстрее, а у см/с – скорость второй точки; тогда получим систему уравнений:
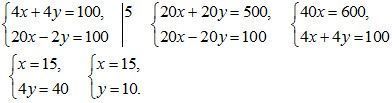
Следовательно, скорость первой точки 15 см/с, а второй – 10 см/с.
Ответ: 15 см/с; 10 см/с.
№ 14.11.
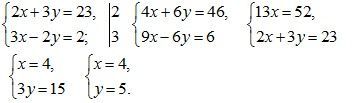
Ответ: 4 ц; 5 ц.
№ 14.12.
На четвертом уроке:
I. Устная работа.
1. Опишите с помощью системы уравнений следующую ситуацию:
а) Разность двух чисел равна 12. Одно из них больше другого в 4 раза;
б) В классе 36 учеников. Девочек на 3 меньше, чем мальчиков;
в) 4 боксера тяжелого веса и 5 боксеров легкого веса вместе весят 730 кг. Спортсмен тяжелого веса весит на 70 кг больше спортсмена легкого веса.
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом
Отзывы
Если у Вас возникли проблемы с программой, обратитесь, пожалуйста, в нашу службу технической поддержки.
- на форуме:
- по электронной почте: soft@uchitel-izd.ru
Опишите проблему подробнее, мы обязательно поможем Вам.









