Алгебра. 7-9 классы: поурочные планы по учебникам Ш.А. Алимова. Программа для установки через Интернет
| Код | СИ-338.2 |
| Авторы-составители | Лебедева Е. Г., Салова Т. А. |
| Издательство | Учитель, 2025 |
| Серия | Поурочное планирование |
| Электронная версия | скачать |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
1. Алгебра. 7 класс : учеб. для общеобразоват. учреждений / Ш. А. Алимов [и др.]. - М. : Просвещение, 2011;
2. Алгебра. 8 класс : учеб. для общеобразоват. учреждений / Ш. А. Алимов [и др.]. - М. : Просвещение, 2011;
3. Алгебра. 9 класс : учеб. для общеобразоват. учреждений / Ш. А. Алимов [и др.]. - М. : Просвещение, 2011.
Материалы, представленные на диске, систематизированы по разделам: "7 класс", "8 класс" и "9 класс".
Целью данного электронного пособия является практическая помощь учителю математики, особенно молодому, в выборе путей построения урока, отвечающего современным требованиям дидактики и практической педагогики.
Специально подобранный дополнительный дидактический материал, проверочные работы и задачи с решениями призваны обеспечить оптимальную насыщенность и высокую эффективность урока.
Предлагаемое распределение материала имеет примерный характер и предполагает творческое применение. Учитель может по своему усмотрению вносить коррективы в ход урока с учетом специфики и уровня подготовки класса. Поурочные конспекты могут также служить дополнением к планам, составленным учителем.
С этим товаром покупают
Примеры документов
Числовые выражения. Урок 1
Числовые выражения
У р о к 1
Цели: повторить и углубить умение учащихся находить значения числовых выражений, составленных из рациональных чисел с помощью знаков сложения, вычитания, умножения и деления; учащиеся должны знать, что выражение, содержащее действие деления на нуль, не имеет смысла.
Ход урока
I. Устные упражнения.
1. Найдите сумму чисел – 3,7 и 6,7; найдите произведение чисел ![]() ; найдите разность чисел
; найдите разность чисел ![]() .
.
2. Я задумал три числа. Найдите первое, если известно, что число, противоположное ему, равно 6. Найдите второе, если число, обратное ему, равно 3. Найдите третье, если известно, что умножив его на ![]() , мы получим 1.
, мы получим 1.
II. Изучение данной темы.
1. Рассмотреть задачу 1 со с. 3.
2. Привести примеры числовых выражений.
3. Если в числовом выражении выполнить указанные действия, то получится число, которое называют ЗНАЧЕНИЕМ этого ЧИСЛОВОГО ВЫРАЖЕНИЯ или, просто, значением выражения.
4. Два числовых выражения, соединенные знаком « = », образуют ЧИСЛОВОЕ РАВЕНСТВО. Если значения левой и правой частей числового равенства совпадают, то равенство называют ВЕРНЫМ.
5. Рассмотреть задачу 2 со с. 4.
Напомним, что сложение и вычитание называют ДЕЙСТВИЯМИ ПЕРВОЙ СТУПЕНИ;
умножение и деление – ДЕЙСТВИЯМИ ВТОРОЙ СТУПЕНИ;
возведение в квадрат и куб – ДЕЙСТВИЯМИ ТРЕТЬЕЙ СТУПЕНИ.
6. Рассмотреть с учащимися принятый ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ с примерами.
7. Выражение, содержащее действие деления на нуль, не имеет смысла.
III. Закрепление изученного материала.
1. Выполнить № 1 самостоятельно с последующей проверкой ответов.
2. Выполнить № 2 самостоятельно.
3. Выполнить на доске и в тетрадях № 3 (1, 3); 4; 8 (1, 3, 5); 9 (устно).
№ 8 (1, 3, 5)
1) 240 · 0,2 = 62 неверно;
3) ![]() верно;
верно;
5) ![]() верно.
верно.
IV. Итоги урока.
Учащиеся повторили и обобщили понятие числового выражения, значения числового выражения, порядок выполнения действий в числовых выражениях.
Домашнее задание. § 1, №№ 3 (2, 4); 8 (2, 4, 6).
№ 8 (2, 4, 6)
2) 18 = 600 · 0,03 верно;
4) ![]() верно;
верно;
6) 12 · 6,5 = 77 неверно.
Алгебраические выражения
Алгебраические выражения
Цели: ввести понятие алгебраического выражения; показать учащимся, как находить значение алгебраического выражения.
Ход урока
I. Проверка домашнего задания (у отдельных учащихся).
II. Устные упражнения.
1. Найдите значения тех выражений, которые имеют смысл:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2. При каких значениях а и b пары (а; 2) и (5; b) равны?
[При а = 5, b = 2].
3. 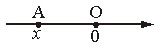
На рисунке показано положение точки А (х) на координатной прямой. Покажите примерно, где на координатной прямой находится точка В (2х), С (–х).
III. Изучение нового материала.
1. Рассмотреть задачу 1 со с. 8.
2. Выражение состоящее из букв, чисел, знаков действий и скобок, называют АЛГЕБРАИЧЕСКИМ ВЫРАЖЕНИЕМ.
3. Если вместо букв, входящих в алгебраическое выражение, подставить некоторые числа и выполнить действия, то полученное в результате число называют ЗНАЧЕНИЕМ АЛГЕБРАИЧЕСКОГО ВЫРАЖЕНИЯ.
IV. Закрепление изученного материала.
Выполнить:
№ 11 (самостоятельно)
№ 12 (1, 3) (в тетрадях)
№ 13 (устно)
№ 14 (1) (на доске и в тетрадях)
№ 15 (самостоятельно)
1) ![]() ;
;
2) 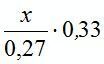 .
.
№ 16 (1) (на доске и в тетрадях)
№ 17 (устно)
№ 18
Решение: ![]() кратно 30. Число единиц должно быть только равно 0, то есть с = 0, тогда b = 2 или b = 5, или b = 8.
кратно 30. Число единиц должно быть только равно 0, то есть с = 0, тогда b = 2 или b = 5, или b = 8.
V. Итоги урока.
Введено понятие алгебраического выражения и значения алгебраического выражения.
Домашнее задание. § 2, №№ 12 (2, 4); 14 (2); 16 (2).
Свойства арифметических действий. Урок 1
Свойства арифметических действий
У р о к 1
Цели: повторить и обобщить свойства арифметических действий, научить записывать данные свойства в краткой форме с помощью букв.
Ход урока
I. Проверка домашнего задания (выборочно).
II. Проверочная работа (7–10 минут).
Вариант I
Стоимость междугородного разговора вычисляется по формуле А = аn, где А – общая стоимость разговора, а – стоимость 1 минуты, n – количество минут.
а) Подсчитайте стоимость междугородного разговора, если а = 8,5 руб., n = 4 мин.
б) Сколько минут длится разговор, если А = 84 руб., а = 7 руб.?
в) Запишите формулу, по которой можно вычислить продолжительность разговора n.
Вариант II
Стоимость покупки вычисляется по формуле С = сm, где
С – стоимость покупки, с – цена 1 кг товара, m – масса товара.
а) Вычислите стоимость купленного сахара, если с = 30 руб., m = 3 кг.
б) Сколько килограммов сахара купили, если С = 70 руб., с =14 руб.?
в) Запишите формулу, по которой можно вычислить массу покупки m.
III. Изучение темы.
1. К арифметическим действиям относят действия сложения, вычитания, умножения и деления.
2. Основные свойства действий обычно называют законами, используя которые, можно обосновать и другие свойства действий.
3. Рассмотреть свойства, приведенные в учебнике на с. 14.
4. Привести примеры использования свойств действий для выполнения преобразований алгебраических выражений с целью их упрощения.
IV. Закрепление изученной темы.
№ 32 (1, 3) выполняется на доске с объяснением.
№ 34 (1, 3, 5) выполняется самостоятельно, с последующей проверкой.
№ 36 (1, 3) выполняется на доске и в тетрадях.
№ 37 (1, 3) выполняется самостоятельно.
V. Итоги урока.
Учащиеся повторили и обобщили знания свойств арифметических действий.
Домашнее задание. § 4, №№ 33 (2, 4); 35 (2, 4); 37 (2, 4).
Правила раскрытия скобок. Урок 1
Правила раскрытия скобок
У р о к 1
Цели: ввести понятие алгебраической суммы; объяснить термин «раскрыть скобки»; научить применению правил раскрытия скобок.
Ход урока
I. Проверка домашнего задания (выборочно).
II. Анализ самостоятельной работы с указанием типичных ошибок.
III. Устные упражнения.
1. Найдите значения выражений:
– (0,7 + 3,2); – 0,7 – 3,2; – (– 0,6 + 1,9); 0,6 – 1,9;
– (4,7 – 3,5); – 4,7 + 3,5.
2. Реактивный самолет расходует а литров горючего на 1000 км пути.
а) Сколько литров горючего расходуется на 3000; 8000; 500; S километров пути?
б) Какой путь пролетит самолет при расходе горючего 5а; 0,1а литров?
IV. Изучение новой темы.
1. АЛГЕБРАИЧЕСКАЯ СУММА – это запись, состоящая из нескольких алгебраических выражений, соединенных знаками «+» или «–».
Например, выражение 8 – 6 + 12 – 4 + 7 – 13 называют алгебраической суммой, так как его можно записать в виде суммы
8 + (–6) + 12 + (–4) + 7 + (–13).
2. Приведем правила раскрытия скобок.
Если к алгебраическому выражению прибавляется алгебраическая сумма, заключенная в скобки, то скобки можно опустить, сохранив знак каждого слагаемого этой алгебраической суммы.
Примеры: а + (b – с – d) = a + b – c – d;
14 + (7 – 23 + 21) = 14 + 7 – 23 + 21.
Если из алгебраического выражения вычитается алгебраическая сумма, заключенная в скобки, скобки можно опустить, изменив знак каждого слагаемого этой алгебраической суммы на противоположный.
Примеры: a – (b – c – d) = a – b + c + d;
14 – (7 – 23 – 21) = 14 – 7 + 23 + 21.
3. Рассмотрим правила заключения в скобки.
Если перед скобкой поставить знак «+», то знаки всех слагаемых, заключенных в скобки, сохраняются.
Примеры: a + b – c + d = a + (b – c + d);
14 + 7 – 13 + 2 = 14 + (7 – 13 + 2).
Если перед скобкой поставить знак «–», то знаки всех слагаемых, заключенных в скобки, меняются на противоположные.
Примеры: a – b – c + d = a – (b + c – d);
14 – 7 + 13 – 2 = 14 – (7 – 13 + 2).
V. Закрепление изученного.
№ 42 (выполнить у доски с объяснением).
№ 43 (самостоятельно, с последующей проверкой).
№ 44 (1, 3).
1) a + (b – (c – d)) = a + b – (c – d) = a + b – c + d;
3) a – ((b – c) – d) = a – (b – c) + d = a – b + c + d.
№ 45 (1, 3).
1) 3a – (a + 2b) = 3a – a – 2b = 2a – 2b.
3) 3m – (5m – (2m – 1)) = 3m – 5m + (2m – 1) = 3m – 5m + 2m – 1 = – 1.
№ 46 (1, 3).
1) a + 2b + m – c = a + 2b + (m – c);
3) a – m – 3c + 4d = a + (– m – 3c + 4d).
№ 47 (1, 3).
1) 2a + 3b + m – c = 2a + 3b – (– m + c);
3) c – m – 2a2 + 3b2 = c – (m + 2a2 – 3b2).
VI. Итоги урока.
Введено понятие алгебраической суммы, сформулированы правила раскрытия скобок и заключения в скобки.
Домашнее задание. § 5, №№ 44 (2, 4), 45 (2, 4), 46 (2, 4), 47 (2, 4).
Правила раскрытия скобок. Урок 2
Правила раскрытия скобок
У р о к 2
Цели: проверить усвоение учащимися изученного материала и продолжить обучение раскрытию скобок.
Ход урока
I. Проверка домашнего задания.
1. Сформулируйте правило раскрытия скобок, перед которыми стоит знак «+».
2. Сформулируйте правило раскрытия скобок, перед которыми стоит знак «–».
3. Сформулируйте правила заключения в скобки.
II. Математический диктант* (см. Примечание).
1. Закончите предложение: «Если раскрываются скобки, перед которыми стоит знак плюс [минус], то знаки слагаемых, стоящих в скобках, …»
2. Раскройте скобки в выражении
x + (c – 0,9); [a – (b – 1,7)].
3. Закончите предложение: «Если раскрываются скобки, перед которыми стоит знак минус [плюс], то знаки слагаемых, стоящих в скобках, …».
4. Раскройте скобки в выражении
а – (– с – 4); [х – (– у – 7)].
5. Запишите выражение а – 4 + х – у [b + 3 – c + y]; заключите его в скобки со знаком плюс [минус] перед скобками.
6. Запишите выражение, равное этому – а + 11 – с + х [– у – 1,3 + а – b], в скобках, перед которыми стоит знак минус [плюс].
III. Выполнение упражнений.
№ 48 (1, 3).
1) (5a – 2b) – (3b – 5a) = 5a – 2b – 3b + 5a = 10a – 5b.
3) ![]() .
.
№ 49 (1, 3).
1) Если с = 0,4 и d = 0,6 , то
![]() ;
;
3) Если ![]() и
и ![]() , то
, то
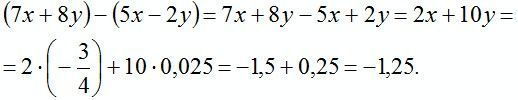
№ 50 (1).
1) Доказать ![]() .
.
Доказательство:
![]() ,
,
так как один из множителей делится на 3, то и произведение 3 (m + n) делится на 3, а значит, и исходная разность тоже делится на 3.
№ 51.
Доказательство:
![]() значение выражения не зависит от а и всегда отрицательно.
значение выражения не зависит от а и всегда отрицательно.
№ 52 (для сильных учащихся).
Дано трехзначное число ![]() .
.
1) ![]()
![]() ;
;
2) ![]()
![]() = 99а – 99с = 99(а – с), так как 99 делится на 9 и на 11, то и произведение 99(а – с) делится на 9 и на 11, это значит, что исходная разность тоже делится на 9 и на 11.
= 99а – 99с = 99(а – с), так как 99 делится на 9 и на 11, то и произведение 99(а – с) делится на 9 и на 11, это значит, что исходная разность тоже делится на 9 и на 11.
IV. Итоги урока. Выставление оценок.
Домашнее задание. § 1–5, №№ 48 (2, 4), 49 (2, 4), 50 (2).
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом









