Геометрия. 7-9 классы: поурочные планы по учебнику А. В. Погорелова. Программа для установки через Интернет
| Код | СИ-265.3 |
| Авторы-составители | Грицаева Н. В., Киселёва Ю. А., Моисеева Е. П. |
| Издательство | Учитель, 2025 |
| Серия | Поурочное планирование |
| Электронная версия | скачать |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
Компакт-диск содержит 3 раздела: "7 класс", "8 класс", "9 класс".
На диске представлены основные теоретические сведения, разнообразный дидактический материал (карточки для устного опроса, таблицы), варианты контрольных работ. Задачи на готовых чертежах присутствуют почти на каждом уроке, представлены различные варианты организации работы с ними. Большинство самостоятельных и контрольных работ сопровождается ответами, указаниями или решениями для более эффективной работы над ошибками. Наличие исторического материала позволит сделать уроки занимательными и интересными.
Представленные разработки помогут начинающим учителям найти свой подход к проведению урока, выбрать оптимальные формы работы, а также будут полезны опытным преподавателям математики и студентам педагогических учебных заведений. Предлагаемое распределение материалов по урокам носит примерный характер, учитель может по своему усмотрению вносить коррективы в ход урока, учитывая специфику и уровень подготовки класса.
С этим товаром покупают
Примеры документов
Урок 1. Геометрические фигуры. Точка и прямая
Основные свойства простейших
геометрических фигур (15 часов)
Цель: систематизировать знания учащихся об основных свойствах простейших геометрических фигур.
Урок 1
Геометрические фигуры. Точка и прямая
Цели: ввести понятия геометрии, планиметрии, простейших фигур; систематизировать сведения учащихся о взаимном расположении прямой и точки; заинтересовать в дальнейшем изучении этого предмета.
Ход урока
I. Организационный момент.
Запись темы урока, формулировка цели.
II. Информация о возникновении и развитии геометрии.
Геометрия возникла в результате практической деятельности людей: нужно было строить жилища, прокладывать дороги, устанавливать границы земельных паев, для этого необходимо было определять их размеры. В переводе с греческого слово «геометрия» означает «землемерие» («гео» – по-гречески земля, а «метрео» – мерить). За несколько столетий до нашей эры в Вавилоне, Египте, Китае и Греции уже существовали простейшие геометрические знания, которые добывались в основном практическим путем. Но они не были собраны в единую систему и передавались от поколения к поколению в виде правил, рецептов, не представляя собой научной теории.
Первым, кто начал получать геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик Фалес (VI в. до н. э.).
Постепенно геометрия становилась наукой, в которой большинство фактов устанавливалось путем выводов, рассуждений, доказательств. Систематизация знаний начались с V века до н. э. Наибольшее влияние на развитие геометрии оказали труды греческого ученого Евклида, жившего в Александрии в III веке до н. э. Сочинения Евклида «Начала» почти 2000 лет служили основной книгой, по которой изучали геометрию. В этой книге была система геометрических сведений, и геометрия впервые предстала как математическая наука.
В геометрии изучали формы, размеры, взаимное расположение предметов и т. д.
На уроках математики вы познакомились с некоторыми геометрическими фигурами и имеете представление, что такое точка, прямая, отрезок, луч, угол, как они могут быть расположены относительно друг друга. Вы знакомы с понятиями: круг, прямоугольник, квадрат, треугольник. Геометрия дает не только понятия о фигурах, но и знакомит со свойствами, которыми они обладают. Школьный курс геометрии делится на два раздела: планиметрию и стереометрию.
Отрезок, луч, прямая, точка, угол, окружность, треугольник, прямоугольник являются плоскими фигурами, потому что они целиком лежат на плоскости (показать фигуры).
Раздел геометрии, изучающий свойства фигур на плоскости, называется планиметрией.
Учащиеся могут записать основные положения в тетрадь.
III. Изучение нового материала.
1. Запись выводов и определений прямой и точек в тетрадь.
Прямые обозначаются малыми латинскими буквами либо двумя большими буквами, соответствующими двум точкам, лежащим на прямой (сделать рисунок в тетради и записать пояснение).
2. Рассматривание рисунков 3 и 4 по учебнику; ввод символов ![]() ; их запись на доске и в тетради.
; их запись на доске и в тетради.
3. Введем первое свойство: какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.
4. Решение задач.
1) Разобрать задачу 3, решенную в учебнике.
2) Решить задачи 1, 2 на с. 19.
5. Проверочная работа (можно на карточках либо в виде математического диктанта).
1) Начертите прямую, назовите ее любой буквой.
2) Отметьте точку на прямой, дав ей название.
3) Начертите две прямые. Отметьте точку, дав ей название, вне прямой (сделать соответствующие записи).
4) Начертите m, n, пересекающиеся в точке D. Поставьте точки, лежащие и не лежащие на этих прямых (сделать соответствующие записи).
IV. Итог урока.
– Сколько прямых можно провести через две точки?
– Сколько общих точек могут иметь две прямые?
– Как обозначаются точки и прямые?
– Что такое геометрия, планиметрия?
Урок 2. Отрезок. Измерение отрезков
Урок 2
Отрезок. Измерение отрезков
Цели: ввести понятие отрезка; научить измерять отрезки, решать задачи с использованием длины отрезка.
Ход урока
I. Организационный момент.
Сообщение темы урока, формулировка цели.
II. Устная работа.
На рисунке (на доске) изображена прямая, на ней отмечены точки ![]() Назовите все образованные прямые и точки, которые лежат на этих прямых и не лежат на них.
Назовите все образованные прямые и точки, которые лежат на этих прямых и не лежат на них.
III. Изучение нового материала.
1. Разобрать рисунки 6, 7 по учебнику. Ввести понятие отрезка, концов отрезка, обозначения отрезка.
Отрезком называется часть прямой, которая состоит из всех точек данной прямой, лежащих между этими точками. Эти точки называются концами отрезка.
2. Введем второе свойство: из трех точек на прямой одна и только одна лежит между двумя другими.
3. Введем третье свойство: каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин его частей, на которые он разбивается любой точкой.
4. Для измерения отрезков используются различные измерительные инструменты (линейка с делениями, циркуль и т. д.). (Показать, как измеряются отрезки.)
IV. Решение задач.
1. Разобрать задачу 9, решенную в учебнике, с подробным оформлением (учить оформлять на доске, объясняя, как из условия задачи выделить, что дано и что требуется доказать).
2. Решить на доске и в тетради задачу 7 (1).
Образец решения.
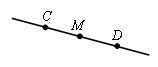
Дано: М CD;
СМ = 2,5 см;
МD = 3,5 см.
Найти: СD.
Решение:
Чтобы найти длину отрезка СD, надо сложить два составляющих отрезка, то есть СМ + МD = СD, значит, 2,5 + 3,5 = 6 (см).
Ответ: СD = 6 см.
3. Решить задачу 5 с оформлением на доске и в тетради.
V. Самостоятельная работа.
Вариант 1: решить задачи 7(2), 10.
Вариант 2: решить задачи 7(3), 11.
Дополнительное задание: решить задачу 15.
VI. Итог урока.
Задание на дом: пункты 3, 4; вопросы 5, 8; задачи 6, 9, 14.
Урок 3. Отрезок. Измерение отрезков
Урок 3
Отрезок. Измерение отрезков
Цели: ввести понятие отрезка; научить измерять отрезки, решать задачи с использованием длины отрезка.
Ход урока
I. Организационный момент.
Сообщение темы урока, формулировка цели.
II. Устная работа.
– Какие геометрические фигуры вам известны?
Возможные ответы учащихся можно записать на доске, распределив их на две группы:
прямая куб
ломаная цилиндр
отрезок шар
луч конус
прямоугольник пирамида
квадрат параллелепипед
многоугольник
– По какому принципу данные геометрические фигуры записаны в двух различных группах? (В первой группе записаны фигуры, существующие на плоскости, а во второй – фигуры, существующие в пространстве.)
1) Начертите прямые а и b, пересекающиеся в точке М. На прямой а отметьте точку Н, отличную от точки М.
а) Являются ли МН и а различными прямыми?
б) Может ли прямая b проходить через точку Н?
III. Решение задач.
1. В треугольнике АВС сторона ВС равна 18 см. Точка М лежит на стороне ВС. Из данных уравнений:
1) 2х + 6 = 18;
2) 2х + 5х = 18;
3) х + 5х = 18;
4) 2х = 5х – выберите такое, которое можно использовать для вычисления длин отрезков ВМ и СМ в следующих случаях:
а) ВМ в 5 раз меньше, чем СМ;
б) ВМ на 5 см меньше, чем СМ;
в) ВМ : СМ = 2 : 5.
2. На отрезке ОР, равном 43 см, взята точка Н. Найдите длину отрезка ОН, если он на 8 см длиннее отрезка РН.
3. Длина отрезка АВ = 6 см, внутри отрезка взята точка М. Найдите длину отрезка ВМ, если:
а) АМ = 2ВМ;
б) 2АМ = 3ВМ;
в) АМ : ВМ = 1 : 5;
г) АМ : ВМ = 3 : 4;
д) АМ – ВМ = 2;
е) 2ВМ + 3АМ = 14.
IV. Итог урока.
Задание на дом:
1. Точки А и В лежат на прямой с. Различны ли прямые АВ и с?
2. Точка С лежит на прямой АВ между А и В. Известно, что отрезок АС на 6 см меньше отрезка ВС. Найдите длины отрезков АС и ВС, если АВ = 24 см.
Точки В, А, С лежат на одной прямой. Может ли точка В разделять точки А и С, если АС = 5 см, а АВ = 7 см?
Урок 4. Полуплоскость. Полупрямая
Урок 4
Полуплоскость. Полупрямая
Цели: ввести понятие полуплоскости, полупрямой; научить различать полупрямые на прямой.
Ход урока
I. Организационный момент.
Формулировка темы и постановка цели урока.
II. Анализ практической работы.
III. Устная работа.
Решение задач по готовым чертежам.

Дано: АВ = 6 см; Дано: МР = 12 см;
ВС = 9 см. КР = 3 см.
Найти: АС. Найти: МК

Дано: DO = 9,3 см. Дано: КС = 9 см, РН = 8 см,
Найдите ошибку. КН = 12 см.
Найти: РС.
IV. Самостоятельная работа (3–5 минут).
Карточка 1
![]()
Дано: КР – РЕ = 3 см, КЕ = 21 см.
Найти: КР и РЕ.
Карточка 2
![]()
Дано: DО = 24 см, ОЕ = 3DО.
Найти: DЕ и ОЕ.
Карточка 3
![]()
Дано: АВ = 28 см, АС : СВ = 4 : 3.
Найти: АС и СВ.
Карточка 4
![]()
Дано: АВ = ВС, СD = DЕ.
Найти: 1) ВD, если АЕ = 20 см;
2) АЕ, если ВD = 12 см.
V. Изучение нового материала.
1. Вспомнить, что такое плоскость. По рисунку 9 учебника ввести понятие полуплоскости.
Прямая, лежащая в плоскости, разбивает ее на две полуплоскости.
2. Ввести четвертое основное свойство: прямая разбивает плоскость на две полуплоскости.
3. Ввести определение полупрямой (луча).
Полупрямой или лучом называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной точки.
4. Дать определение начальной точки, ввести определение дополнительных полупрямых.
Данная точка, от которой исходит луч, называется начальной точкой. Различные полупрямые одной и той же прямой, имеющие общую начальную точку, называются дополнительными полупрямыми.
5. Объяснить рисунок 12, зарисовать в тетрадь, сделать соответствующие записи.
VI. Решение задач.
Решить задачи 18, 20, 21.
VII. Итог урока.
– Назовите различие луча и полупрямой.
– Что такое дополнительная полупрямая?
– Что такое начальная точка?
– Что такое полуплоскость и в чем ее отличие от плоскости?
Задание на дом: пункты 5, 6; вопросы 11, 12; разобрать задачи 17, 22; решить задачи 13, 19.
Урок 6. Угол
Урок 6. Угол
Цели: ввести понятие угла; рассмотреть различные виды углов; научить измерять углы.
Ход урока
I. Организационный момент.
Формулировка темы и постановка цели урока.
II. Самостоятельная работа (10 минут).
Вариант 1
1. На прямой b отмечены точки С, D, Е так, что CD = 6 см, DЕ = 8 см. Какой может быть длина отрезка СЕ?
2. Точка М – середина отрезка АВ; МВ = 5 дм. Найдите длину отрезка АВ.
Вариант 2
1. На прямой m отмечены точки А, В, С так, что АС = 12 см, АВ = 8 см. Какой может быть длина отрезка ВС?
2. Точка Р – середина отрезка MN. Найдите длину отрезка PN, если MN = 14 дм.
Два ученика работают по карточкам у доски.
Карточка 1
Точка N лежит на прямой MK между точками M и K. Найдите расстояние между серединами отрезков MN и NK, если MN = 7 см, NK = 12 см.
Карточка 2
На отрезке ОР, равном 42 см, взята точка Н. Найдите длину отрезка ОН, если он на 8 см длиннее отрезка РН.
IV. Изучение нового материала.
1. Запись определения. Углом называется фигура, которая состоит из точки – вершины угла – и двух различных полупрямых, исходящих из этой точки, – сторон угла.
2. Вводятся различные способы обозначения угла.
Угол может обозначаться несколькими способами:
РО, Р(ab), РFDC.
3. Вводятся понятия углов (развернутый, неразвернутый) по рис. 14, 15 учебника (зарисовать в тетрадь).
Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.
4. Записать определения тупого угла, острого угла, прямого угла и зарисовать.
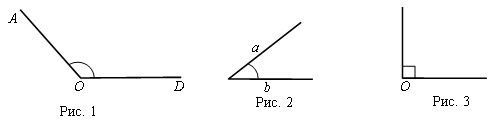
РАОD, тупой угол – это угол, градусная мера которого превышает 90° (рис. 1).
Р(ab), острый угол – это угол, градусная мера которого меньше 90° (рис. 2).
РО, прямой угол – это угол, градусная мера которого равна 90° (рис. 3).
5. Записать в тетрадь основное пятое свойство: каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
V. Решение задач.
Задача 1. Дано: РАОВ = 45°, РВОС = 21°.
Найти РАОС.
Задача 2. Дано: РEDK = 36°.
Найти: РFDK.
VI. Итог урока.
- Что такое угол?
- Что такое развернутый, неразвернутый угол?
- Какие еще углы вы знаете?
- Какими единицами измеряются углы?
- Сформулировать основное пятое свойство.
- Из чего состоит угол?
Задание на дом: пункт 7; вопросы 13–19; задача 26.
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом









