Алгебра 8-9 классы: поурочные планы по учебникам под редакцией Г. В. Дорофеева. Программа для установки через Интернет
| Код | СИ-258.2 |
| Авторы-составители | Видеман Т. Н., Дюмина Т. Ю. |
| Издательство | Учитель, 2025 |
| Серия | Поурочное планирование |
| Электронная версия | скачать |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
1. Алгебра. 8 класс: учебник для общеобразовательных учреждений / Г. В. Дорофеев [и др.]; под ред. Г. В. Дорофеева; Рос. акад. наук, Рос. акад. образования, изд-во "Просвещение". - М. : Просвещение, 2009.
2. Алгебра. 9 класс: учебник для общеобразовательных учреждений / Г. В. Дорофеев [и др.]; под ред. Г. В. Дорофеева; Рос. акад. наук, Рос. акад. образования, изд-во "Просвещение". - М. : Просвещение, 2009.
Представленные в пособии поурочные планы включают теоретические сведения, методические рекомендации к объяснению нового материала, задания для устной работы, математические диктанты, тесты, проверочные и самостоятельные работы, игровые формы работы, дополнительные материалы к урокам и др. Также в пособии рассматриваются математические задачи и предлагаются способы их решения.
Предлагаемое распределение материала в конспектах уроков носит примерный характер. Учитель может по своему усмотрению вносить коррективы в ход урока с учетом специфики и уровня подготовки класса. Поурочные планы, представленные на диске, могут служить дополнением к планам, составленным учителем.
С этим товаром покупают
Примеры документов
Урок 1. Понятие алгебраической дроби
Урок 1
Понятие алгебраической дроби
Цели: ввести понятие алгебраической дроби, формировать умение составлять алгебраические дроби и искать их значения при заданных значениях переменных.
Ход урока
I. Организационный момент.
II. Устная работа.
– Назовите дробь, соответствующую данному частному:
а) 4 : 9; д) –3 : 8;
б) 15 : 7; е) 5 : (–11);
в) 10 : 20; ж) –2 : (–6);
г) 12 : 16; з) –9 : 15.
III. Объяснение нового материала.
Последовательность объяснения:
1. Обратиться к записи частного двух целых чисел в виде обыкновенной дроби для проведения аналогии с записью многочленов в виде частного.
2. Показать, что частное двух многочленов не всегда является многочленом.
3. Дать определение алгебраической дроби.
В процессе проведения устной работы у учащихся была возможность вспомнить, как частное двух целых чисел выражается дробью. При изложении нового материала проводится параллель с целыми числами.
Перед введением понятия алгебраической дроби необходимо рассмотреть пример из учебника, показывающий, что не всегда частное двух многочленов является многочленом. Этот пример не только помогает установить данный факт, но и является полезной развивающей задачей.
Алгебраическая дробь вводится как способ записи частного двух многочленов. Необходимо обратить внимание учащихся на то, что любое целое число можно представить в виде дроби, также и любой многочлен представляется в виде дроби со знаменателем 1.
На последнем этапе вводится определение алгебраической дроби.
Определение. Алгебраической дробью называется дробь, числитель и знаменатель которой представлены многочленами.
После введения данного определения дать учащимся задание на распознание алгебраических дробей.
Задание: Определите, какие из данных выражений являются алгебраическими дробями. Ответ объясните.
а) 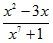 ; г)
; г) ![]() ;
;
б) ![]() ; д) ax – 2;
; д) ax – 2;
в) ![]() ; е)
; е) 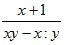 .
.
IV. Формирование умений и навыков.
Все задания, выполняемые учащимися на этом уроке, можно условно разбить на три группы.
1. Использование понятия алгебраической дроби при ее записи.
2. Нахождение значений дроби при заданных значениях переменных.
3. Составление алгебраических дробей по каким-либо условиям.
Упражнения:
№ 1 (а, в).
№ 2 (а, в). – Выполнение данного упражнения целесообразно начать с числовых примеров: 48 : 4 = 12, поскольку 4 · 12 = 48. Это даст учащимся возможность осознанно подойти к выполнению задания.
№ 3 (а, в, д). При выполнении каждого задания можно вызвать к доске сразу нескольких учащихся. У каждого из них получатся разные выражения. После нахождения этих выражений сделать ряд выводов:
– в качестве искомого выражения можно взять произведение данных выражений;
– выражений, удовлетворяющих условию задания, бесконечно много.
№ 4 (а, в), № 6 (а, г), № 12 (а, г). При вычислении необходимо следить за грамотной записью учащихся на доске и у себя в тетрадях. В № 12 выражение сначала нужно упростить.
г) 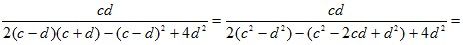
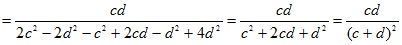
при с = –1 и d = 11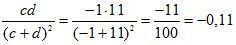 .
.
№ 15 (а). В случае затруднения учащихся при выполнении данного задания нужно напомнить им, что для выражения переменной из формулы достаточно рассматривать эту переменную или выражение, в которое она входит как неизвестный множитель (слагаемое, делитель и т. д.).
V. Итоги урока.
Урок 2. Множество допустимых значений переменных, входящих в дробь
Урок 2
МНОЖЕСТВО ДОПУСТИМЫХ ЗНАЧЕНИЙ ПЕРЕМЕННЫХ,
ВХОДЯЩИХ В ДРОБЬ
Цель: формировать умение находить множество допустимых значений переменных, входящих в дробь.
Ход урока
I. Организационный момент.
II. Устная работа.
– Подставьте вместо * какое-нибудь число и назовите полученную дробь.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
При выполнении этой работы необходимо подвести учащихся к мысли о том, что вместо * нельзя подставлять число, обращающее знаменатель в нуль.
III. Объяснение нового материала.
Объяснение материала проходит в три этапа:
1. Актуализация знаний учащихся.
2. Рассмотрение вопроса о том, всегда ли алгебраическая дробь имеет смысл.
3. Вывод алгоритма нахождения множества допустимых значений переменных, входящих в дробь.
При актуализации знаний учащимся можно задать следующие вопросы:
– Какую дробь называют алгебраической?
– Может ли в знаменателе алгебраической дроби стоять целое число?
– Как найти значение алгебраической дроби при заданных значениях входящих в нее переменных?
Для выяснения вопроса о допустимых значениях переменных дроби можно предложить учащимся выполнить следующее задание.
Задание: найдите значение дроби при указанных значениях переменной.
![]() при х = 4; 0; 1.
при х = 4; 0; 1.
Выполняя данное задание, учащиеся понимают, что при х = 1 невозможно найти значение дроби. Это позволяет им сделать следующий вывод: в алгебраическую дробь нельзя подставлять числа, которые обращают ее знаменатель в нуль (этот вывод должен быть сформулирован и произнесен вслух самими учащимися).
После этого учитель сообщает учащимся, что все числа, которые можно подставлять в алгебраическую дробь, образуют множество допустимых значений переменных, остальные же числа в это множество не входят.
Для вывода алгоритма нахождения множества допустимых значений переменных дроби учитель просит учащихся, опираясь на вывод, сделанный ими ранее, ответить на ряд вопросов:
– Как узнать, какие числа не входят в множество допустимых значений переменных дроби? (Нужно найти числа, обращающие знаменатель дроби в нуль.)
– Как найти числа, при которых знаменатель алгебраической дроби равен нулю? (Приравнять его к нулю и решить полученное уравнение.)
После этого обратить внимание учащихся на таблицу, помещенную на с. 5 учебника. В ней содержатся почти все типы дробей, для которых учащиеся должны уметь указывать множество допустимых значений переменных.
IV. Формирование умений и навыков.
№ 7 (а, в, д, ж). Ответы на вопрос об области допустимых значений переменных, входящих в дробь, могут звучать по-разному. Например: рассматривая дробь ![]() , можно сказать, что допустимыми значениями переменной являются все числа, кроме с = –2, или, что в множество допустимых значений переменной не входит число –2. И та и другая формулировки являются верными, главное – следить за правильностью записи ответа и оформлением решения заданий.
, можно сказать, что допустимыми значениями переменной являются все числа, кроме с = –2, или, что в множество допустимых значений переменной не входит число –2. И та и другая формулировки являются верными, главное – следить за правильностью записи ответа и оформлением решения заданий.
№ 13 (а, в, д).
Решение:
а) 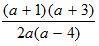
2а(а – 4) ≠ 0
2а ≠ 0 или а – 4 ≠ 0
а ≠ 0 а ≠ 4
Ответ: а ≠ 0 и а ≠ 4.
в) 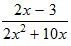
2x2 + 10x ≠ 0
2x(x + 5) ≠ 0
2x ≠ 0 или x + 5 ≠ 0
x ≠ 0 x ≠ –5
Урок 2/4. Сокращение дробей
Цель: формировать умение применять основное свойство дроби при сокращении дробей.
Ход урока
I. Организационный момент.
II. Устная работа.
– Назовите дробь, которая получится после сокращения данной:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
III. Проверочная работа.
Вариант I
1. Разделите числитель и знаменатель дроби на указанное число:
а) ![]() на 3; б)
на 3; б) ![]() на 3.
на 3.
2. Умножьте числитель и знаменатель дроби на указанное число:
а) ![]() на а; б)
на а; б) ![]() на а; в)
на а; в) 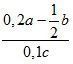 на 10.
на 10.
Вариант II
1. Разделите числитель и знаменатель дроби на указанное число:
а) ![]() на 7; б)
на 7; б) ![]() на 7.
на 7.
2. Умножьте числитель и знаменатель дроби на указанное число:
а) ![]() на n; б)
на n; б) ![]() на n; в)
на n; в) 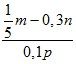 на 10.
на 10.
IV. Формирование умений и навыков.
Для успешной работы учащихся на уроке им необходимо не только использовать основное свойство дроби, но и применять ряд других знаний и умений, полученных и сформированных ранее.
Учащиеся должны помнить формулы сокращенного умножения и основные приемы разложения многочлена на множители. Поэтому формирование умения сокращать алгебраические дроби следует начать с актуализации знаний.
Вопросы учащимся:
1. Можно ли начать сокращение дроби 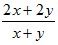 в том виде, в котором она записана? (Нет.)
в том виде, в котором она записана? (Нет.)
2. Что нужно сделать, чтобы сократить эту дробь? (В числителе вынести за скобки 2.)
3. Какое действие необходимо выполнить, чтобы сократить любую дробь? (Разложить на множители числитель и знаменатель этой дроби.)
4. Какие существуют приемы разложения многочлена на множители?
1) Вынос общего множителя за скобки;
2) применение формул сокращенного умножения;
3) метод группировки.
Задание: разложите на множители многочлен:
а) x2y – 2x; д) x2 + 6x + 9;
б) 3a2b – 9ab2; е) a2 – 10a + 25;
в) m2 – 4n2; ж) ax + bx + ay + by;
г) a3 – a; з) ab – b + 3a – 3.
После проведения такой работы можно приступить к непосредственному сокращению дробей.
1. № 24 (а, в), № 25 (в, д), № 27 (а, в, д).
2. № 29 (а, в, д), № 36 (а, в, д). Необходимо подвести учащихся к мысли о том, что при разложении многочлена на множители нужно начинать с выноса общего множителя за скобки, иначе можно не увидеть формулу сокращенного умножения.
№ 36.
в) 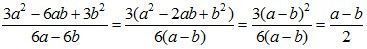 .
.
3. Найдите значение дроби:
а) 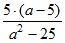 при а = –4,5; б)
при а = –4,5; б) 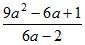 при а = 1,8;
при а = 1,8;
в) 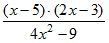 при х = –0,2;
при х = –0,2;
г) 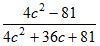 при с = 2,5.
при с = 2,5.
4. № 38 (а, в, д).
Решение:
Урок 3/5. Следствия из основного свойства дроби
Урок 3/5
следствия из основного свойства дроби
Цели: продолжить формирование умения сокращать дроби; вывести следствия из основного свойства дроби и формировать умение применять их при сокращении дробей.
Ход урока
I. Организационный момент.
II. Устная работа.
– Назовите дробь, которая получится после сокращения данной:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
III. Проверочная работа.
Вариант I
1. Приведите дроби к указанному знаменателю:
а) 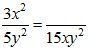 ;
;
б) 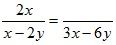 ;
;
в) 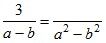 .
.
2. Сократите дробь:
а) ![]() ; б)
; б) ![]() .
.
Вариант II
1. Приведите дроби к указанному знаменателю:
а) 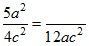 ;
;
б) ![]() ;
;
в) 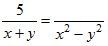 ;
;
2. Сократите дробь.
а) ![]() ; б)
; б) 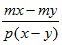 .
.
IV. Объяснение нового материала.
Специальное внимание на этом уроке необходимо уделить следствиям из основного свойства дроби.
При объяснении материала следует провести аналогию с обыкновенными дробями. Для этого целесообразно предложить учащимся выполнить задание: среди данных дробей найти такие, которые равны ![]() ; ответ объяснить.
; ответ объяснить.
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Здесь же следует вспомнить, что знак «минус» перед дробью можно записывать как перед числителем, так и перед знаменателем. Для этого дать учащимся такое задание: среди данных дробей найти такие, которые равны ![]() ; ответ объяснить.
; ответ объяснить.
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
После выполнения этих заданий можно перейти к буквенной записи следствий из основного свойства дроби:
![]() .
.
Необходимо, чтобы учащиеся знали и осознавали формулировки этих следствий. В случае затруднений можно продемонстрировать практическое применение следствий и дать их более прикладную к задачам формулировку:
1. Знак «минус» перед дробью можно вносить либо в числитель, либо в знаменатель дроби.
Пример:
![]() .
.
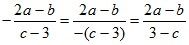 .
.
2. Знак «минус» из числителя или знаменателя дроби можно выносить за знак дроби.
Пример:
![]() ;
;
Урок 1/6. Сложение и вычитание дробей с одинаковыми знаменателями
Урок 1/6
сложение и вычитание дробей
с одинаковыми знаменателями
Цель: формировать умение складывать и вычитать алгебраические дроби с одинаковыми знаменателями.
Ход урока
I. Организационный момент.
II. Проверочная работа.
Вариант I
Сократите дроби:
а) 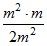 ; б)
; б) 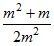 ; в)
; в) 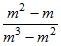 ;
;
г) 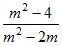 ; д)
; д) ![]() .
.
Вариант II
Сократите дроби:
а) ![]() ; б)
; б) 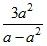 ; в)
; в) 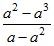 ;
;
г) 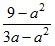 ; д)
; д) ![]() .
.
III. Устная работа.
Вычислите сумму или разность дробей:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
IV. Объяснение нового материала.
Устная работа дает возможность актуализировать знания учащихся о сложении и вычитании обыкновенных дробей с одинаковыми знаменателями.
После этой работы следует сообщить учащимся, что алгебраические дроби с одинаковыми знаменателями складываются и вычитаются по тем же правилам, которые учащиеся способны сформулировать самостоятельно.
После формулировки правил на доску выносится их буквенная запись:
![]() и
и ![]() .
.
На этом уроке не следует рассматривать вопрос о сложении и вычитании дробей с разными знаменателями. Сначала учащиеся должны отработать навык записи суммы и разности дробей, восстановить навыки раскрытия скобок и приведения подобных слагаемых.
Однако во второй половине урока можно разобрать случай, когда складываются или вычитаются дроби, у которых знаменатели являются противоположными выражениями.
V. Формирование умений и навыков.
1. № 44 (а, в), № 45 (а, в), № 46 (а, в, д), № 47 (а, в, д).
При вычитании дробей учащиеся могут допускать распространенную ошибку: не учитывать, что знак «минус» ставится перед всем числителем вычитаемой дроби, и неправильно расставлять знаки.
Поэтому важно следить, чтобы первое время учащиеся вели подробные записи.
№ 47.
в) 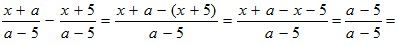 1.
1.
д) 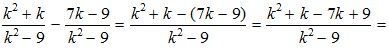
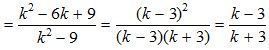 .
.
2. Представьте выражение в виде дроби:
а) 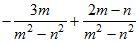 ;
;
б) 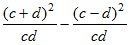 ;
;
в) 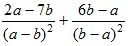 ;
;
г) 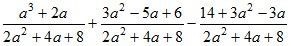 .
.
3. Выполните сложение или вычитание дробей:
а) ![]() ;
;
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом









