Алгебра. 9 класс: поурочные планы по учебнику Ю. Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.Б. Суворовой. Программа для установки через Интернет
| Код | СИ-223.4 |
| Авторы-составители | Дюмина Т. Ю., Махонина А. А. |
| Издательство | Учитель, 2025 |
| Серия | Поурочное планирование |
| Электронная версия | скачать |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
Алгебра. 9 класс : учеб. для общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова ; под ред. С. А. Теляковского. - М. : Просвещение, 2012.
Конспекты уроков, представленные на диске, систематизированы по разделам в соответствии с распределением учебного материала в учебнике. Предлагаемые поурочные планы включают теоретические материалы, алгебраические задачи с решениями и ответами, задания для устной работы, тесты, проверочные и контрольные работы и др. В каждом из разделов предложены методические рекомендации к объяснению нового материала. Предлагаемое пособие окажет практическую помощь учителю математики, особенно молодому, в выборе путей построения урока, отвечающего современным требованиям, в подборе дополнительного дидактического материала и проведении проверочных работ, а также может быть полезно студентам педагогических учебных заведений, слушателям ИПК.
С этим товаром покупают
Примеры документов
Урок 1. Ключевые задачи на функцию
У р о к 1 .
Ключевые задачи на функцию
Цели: обобщить имеющиеся у учащихся знания о функциях; выделить ключевые задачи на функцию.
Ход урока
I. Организационный момент.
II. Устная работа.
Найдите значение выражения: 1 – 3а2 при а = 0; а = 1; а = –1; а = –![]() .
.
III. Объяснение нового материала.
На этом уроке целесообразно повторить те сведения о функциях, которые уже известны учащимся, обобщить и систематизировать эти сведения, выделить ключевые задачи на функцию. Вопросы о нахождении области определения и области значений функции лучше разобрать на следующем уроке.
После объяснения материала у учащихся в тетрадях должны быть записаны следующие сведения о функциях:
1. Определение функции.
2. Смысл записи у = f (x).
3. Определение графика функции.
4. Формулы ранее изученных функций и их графики.
Далее необходимо выделить основные задачи, связанные с функциями:
№ 1. По данному значению аргумента найти значение функции.
№ 2. Найти те значения аргумента, которые соответствуют данному значению функции.
№ 3. Найти точки пересечения графика функции с осями координат.
№ 4. Найти точки пересечения графиков данных функций.
№ 5. Найти все значения аргумента, при каждом из которых график одной функции лежит выше (ниже) графика другой функции.
Эти задачи учащиеся должны уметь решать без построения графиков функций.
IV. Формирование умений и навыков.
1. № 1, № 2, № 4 – нахождение значений функции при заданных значениях аргумента.
2. № 5, № 6 (а), № 7 – нахождение значений аргумента при заданных значениях функции.
3. № 13.
4. Даны функции: f (x) = 2х + 1 и g (х) = 3– х. Найдите:
а) f (–5); g (7); f (g (3)); g (f (2)).
б) Значение х, при которых g (х) = 5.
в) Точки пересечения графиков данных функций с осями координат.
г) Координаты точки, в которой пересекаются графики данных функций.
д) Все точки, в которых график функции у = f (x) лежит ниже графика функции у = g (x).
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что такое функция?
– Что называется графиком функции?
– Как найти точки пересечения графиков двух функций, не строя эти графики?
– Как найти точки пересечения графика функции с осями координат?
– Как найти все точки, в которых график одной функции лежит выше или ниже графика другой функции?
Домашнее задание.
1. № 3, № 6 (б), № 8, № 12.
2. Даны функции: f (x) = х2 – 2х и g (x) = 3х – 4. Найдите:
а) f (–2); g (–10); f (g (–1)).
б) Значения х, при которых f (x) = 3.
в) Точки пересечения графиков данных функций с осями координат.
г) Координаты точек, в которых пересекаются графики данных функций.
д) Все точки, в которых график функции у = f (x) лежит выше графика функции у = g (x).
Урок 6. Нахождение свойств функции по формуле и по графику
У р о к 6.
Нахождение свойств функции
по формуле и по графику
Цели: обобщить и систематизировать знания учащихся о свойствах функции; продолжить формирование умения находить свойства функции по их формуле или графику.
Ход урока
I. Организационный момент.
II. Устная работа.
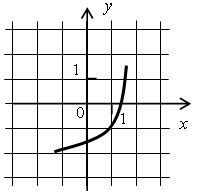
Определите, какие из функций, изображенных на рисунках, обладают следующими свойствами:
а) имеют область определения [–3; 3];
б) имеют область значений [–2; 2];
в) имеют два нуля;
г) принимают только отрицательные значения;
д) являются возрастающими;
е) являются убывающими.
1) 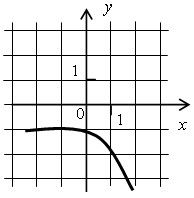 2)
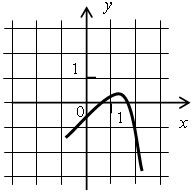
2) 
3) 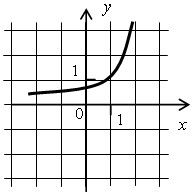 4)
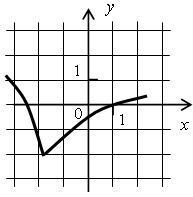
4) 
5) 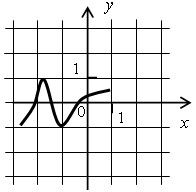 6)
6) 
III. Формирование умений и навыков.
Все задания, которые будут выполнять учащиеся на этом уроке, можно разбить на две группы. В первую группу войдут задания на перечисление свойств функции по ее графику. Во второй группе будут задания на нахождение свойств функции по задающим их формулам. После выполнения каждой группы заданий необходимо, чтобы учащиеся сделали выводы: как найти свойства функции в том или ином случае, то есть по графику или по формуле.
Упражнения:
1-я г р у п п а.
Функции у = f (х) и у = g (х) заданы своими графиками:
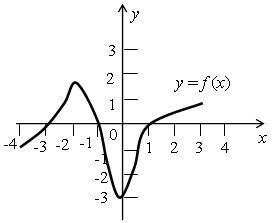
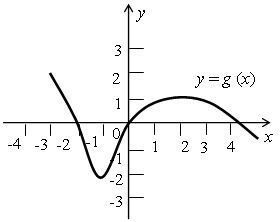
Перечислите свойства функций и сформулируйте вывод о том, как могут быть найдены свойства любой функции по ее графику.
2-я г р у п п а.
1. Найдите нули функции (если они существуют):
а) у = –3х + 1,8; в) у = ![]() ;
;
б) у = ![]() ; г) у = 16 х2.
; г) у = 16 х2.
2. № 43 (а).
Урок 7. Нахождение корней квадратного трехчлена
У р о к 7.
Нахождение корней квадратного трехчлена
Цели: ввести понятие квадратичного трехчлена и его корней; формировать умение находить корни квадратного трехчлена.
Ход урока
I. Организационный момент.
II. Устная работа.
Какие из чисел: –2; –1; 1; 2 – являются корнями уравнений?
а) 8х + 16 = 0; в) х2 + 3х – 4 = 0;
б) 5х2 – 5 = 0; г) х3 – 3х – 2 = 0.
III. Объяснение нового материала.
Объяснение нового материала проводить по следующей с х е м е:
1) Ввести понятие корня многочлена.
2) Ввести понятие квадратного трехчлена и его корней.
3) Разобрать вопрос о возможном количестве корней квадратного трехчлена.
Вопрос о выделении квадрата двучлена из квадратного трехчлена лучше разобрать на следующем уроке.
На каждом этапе объяснения нового материала необходимо предлагать учащимся устное задание на проверку усвоения основных моментов теории.
З а д а н и е 1. Какие из чисел: –1; 1; ![]() ; 0 – являются корнями многочлена х4 + 2х2 – 3?
; 0 – являются корнями многочлена х4 + 2х2 – 3?
З а д а н и е 2. Какие из следующих многочленов являются квадратными трехчленами?
1) 2х2 + 5х – 1; 6) х2 – х – ![]() ;
;
2) 2х – ![]() ; 7) 3 – 4х + х2;
; 7) 3 – 4х + х2;
3) 4х2 + 2х + х3; 8) ![]() х + 4х2;
х + 4х2;
4) 3х2 – ![]() ; 9)
; 9) ![]() + 3х – 6;
+ 3х – 6;
5) 5х2 – 3х; 10) 7х2.
Какие из квадратных трёхчленов имеют корень 0?
З а д а н и е 3. Может ли квадратный трехчлен иметь три корня? Почему? Сколько корней имеет квадратный трехчлен х2 + х – 5?
IV. Формирование умений и навыков.
Упражнения:
1. № 55, № 56, № 58.
2. № 59 (а, в, д), № 60 (а, в).
3. № 61.
В этом задании не нужно искать корни квадратных трехчленов. Достаточно найти их дискриминант и ответить на поставленный вопрос.
а) 5х2 – 8х + 3 = 0;
D1 = 16 – 15 = 1;
D1 > 0, значит, данный квадратный трехчлен имеет два корня.
б) 9х2 + 6х + 1 = 0;
D1 = 9 – 9 = 0;
D1 = 0, значит, квадратный трехчлен имеет один корень.
в) –7х2 + 6х – 2 = 0;
7х2 – 6х + 2 = 0;
D1 = 9 – 14 = –5;
D1 < 0, значит, квадратный трехчлен не имеет корней.
Если останется время, можно выполнить № 63.
Р е ш е н и е
Пусть ax2 + bx + c – данный квадратный трехчлен. Поскольку a + b +
+ c = 0, то один из корней этого трехчлена равен 1. По теореме Виета второй корень равен ![]() . Согласно условию, с = 4а, поэтому второй корень данного квадратного трехчлена равен
. Согласно условию, с = 4а, поэтому второй корень данного квадратного трехчлена равен ![]() .
.
О т в е т: 1 и 4.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что такое корень многочлена?
– Какой многочлен называют квадратным трехчленом?
– Как найти корни квадратного трехчлена?
– Что такое дискриминант квадратного трехчлена?
– Сколько корней может иметь квадратный трехчлен? От чего это зависит?
Домашнее задание: № 57, № 59 (б, г, е), № 60 (б, г), № 62.
Урок 8. Выделение квадрата двучлена из квадратного трехчлена
У р о к 8.
Выделение квадрата двучлена
из квадратного трехчлена
Цели: формировать у учащихся умение выделять квадрат двучлена из квадратного трехчлена и решать задачи с помощью этого преобразования.
Ход урока
I. Организационный момент.
II. Устная работа.
Какие из чисел: –2; –1; 0; 1; 2 – являются корнями квадратных трехчленов х2 + 4х + 3 и 5х – 2х2?
III. Объяснение нового материала.
В 8 классе учащиеся уже решали квадратные уравнения с помощью выделения квадрата двучлена из квадратного трехчлена, то есть данный прием им знаком. Однако следует еще раз разобрать несколько примеров и записать алгоритм, по которому выполняется это преобразование.
Сначала лучше привести несложный пример, где коэффициент а квадратного трехчлена равен 1, а коэффициент b – четный:
х2 – 6х + 4 = х2 – 2 · 3 · х + 32 – 32 + 4 = (х – 3)2 – 5.
Затем нужно разобрать сложный пример. При этом учащиеся записывают в тетрадях проводимые преобразования и их словесное описание в общем виде, то есть составляют алгоритм выделения квадрата двучлена из квадратного трехчлена.
ax2 + bx + c 2х2 + 16х + 5
1) Вынести за скобки коэффициент а:
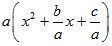
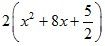
2) Представить выражение ![]() в виде удвоенного произведения двух множителей:
в виде удвоенного произведения двух множителей:
![]() 8х = 2 · 4 · х
8х = 2 · 4 · х
3) К выражению в скобках прибавить и вычесть 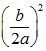 :
:
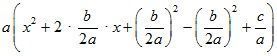
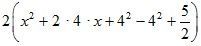
4) Представить часть выражения в скобках в виде полного квадрата:
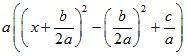
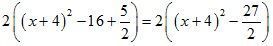
5) Раскрыть скобки:
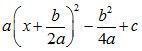 ; 2 (х + 4)2 – 27;
; 2 (х + 4)2 – 27;
2х2 + 16х + 5 = 2 (х + 4)2 – 27.
Далее следует разобрать пример 3 из учебника, который показывает, как прием выделения квадрата двучлена из квадратного трехчлена может быть использован при решении геометрической задачи.
IV. Формирование умений и навыков.
Упражнения:
1. № 64, № 66.
2. № 68.
Р е ш е н и е
Выделим квадрат двучлена из данного квадратного трехчлена:
2х2 – 4х + 6 = 2 (х2 – 2х + 3) = 2 (х2 – 2 · 1 · х + 12 – 12 + 3) = 2 ((х – 1)2 +
+ 2) = 2 (х – 1)2 + 4.
Выражение 2 (х – 1)2 положительно при любом х ≠ 1, поэтому сумма 2 (х – 1)2 + 4 принимает наименьшее значение при х = 1 и это значение равно 4.
О т в е т: при х = 1 наименьшее значение равно 4.
3. № 70.
Р е ш е н и е
Пусть один катет треугольника равен х см. Тогда второй катет равен (6 – х) см, а площадь треугольника равна ![]() x (6 – x) см2.
x (6 – x) см2.
Раскрыв скобки в выражении ![]() x (6 – x), получим 3х –
x (6 – x), получим 3х – ![]() x2. Выражение –
x2. Выражение –![]() x2 + 3х является квадратным трехчленом. Выделим из него квадрат двучлена:
x2 + 3х является квадратным трехчленом. Выделим из него квадрат двучлена:
–![]() x2 + 3х = –
x2 + 3х = –![]() (х2 – 6х) = –
(х2 – 6х) = –![]() (х2 – 2 · 3 · х + 32 – 32) = –
(х2 – 2 · 3 · х + 32 – 32) = –![]() ((х – 3)2 – 9) =
((х – 3)2 – 9) =
Урок 10. Применение теоремы о разложении квадратного трехчлена на множители для преобразования выражений
У р о к 10.
Применение теоремы о разложении
квадратного трехчлена на множители
для преобразования выражений
Цель: продолжить формирование умения раскладывать на множители квадратный трехчлен, применяя это разложение для сокращения дробей и упрощения выражений.
Ход урока
I. Организационный момент.
II. Устная работа.
Определите, можно ли представить квадратный трехчлен в виде произведения многочленов первой степени:
а) 2х2 + х – 5; г) х2 – 2х + 8;
б) 2х2 + х + 5; д) х2 – 2х – 8;
в) х2 – 4х + 4; е) 9х2 + 6х + 1.
III. Формирование умений и навыков.
На этом уроке следует обобщить знания учащихся о различных способах разложения многочленов на множители. Особое внимание нужно уделить двум вопросам:
1) Сколько существует способов разложения многочленов на множители и в чем они заключаются?
2) При решении каких задач пригодится умение раскладывать многочлен на множители?
Поскольку для сокращения дробей и упрощения выражений учащимся потребуется знание всех способов разложения многочленов на множители, то для начала необходимо актуализировать эти знания.
Учитель сообщает учащимся, что теперь им известны все основные способы разложения многочленов на множители и просит перечислить эти способы. В тетрадях у учащихся должны быть записаны названия всех четырех способов и приведены примеры.
1. Вынос общего множителя за скобки:
а) 2х3 + 5х2 – х = х (2х2 + 5х – 1);
б) 9х5 + 15х3 = 3х3 (3х2 + 5).
2. Применение формул сокращенного умножения:
а) 4х2 – у2 = (2х – у) (2х + у);
б) х2 – 6х + 9 = (х – 3)2;
в) х3 + 8 = (х + 2) (х2 – 2х + 4).
3. Метод группировки:
а) 6х3 – 8х2 + 3х – 4 = 2х2 (3х – 4) + (3х – 4) = (3х – 4) (2х2 + 1);
б) 2х + у + у2 – 4х2 = 2х + у + (у – 2х) (у + 2х) = (у + 2х) (1 + у – 2х).
4. Разложение на множители квадратного трехчлена:
а) х2 – 4х – 5 = (х + 1) (х + 5);
б) 3х2 + х – 4 = 3 (x – 1)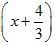 = (х – 1) (3х + 4).
= (х – 1) (3х + 4).
Далее выделяются две основные группы заданий, при выполнении которых необходимо умение раскладывать многочлен на множители:
– сокращение дробей;
– упрощение выражений.
Упражнения:
1-я г р у п п а.
1. № 83 (а, в, д), № 85 (а).
2. Сократите дробь:
а) ![]() ; б)
; б) 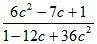 .
.
Р е ш е н и е
а) 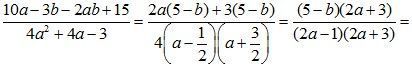
![]()
б) 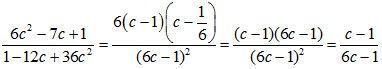 .
.
2-я г р у п п а.
Упростите выражение:
а) 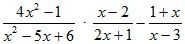 ;
;
б) 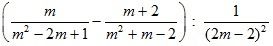 .
.
Р е ш е н и е
а) 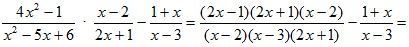
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом









