Математика. 3-4 классы: поурочные планы по программе "Школа 2100". Программа для установки через Интернет
| Код | СИ-235.4 |
| Авторы-составители | Бут Т. В., Тургаева М. М. |
| Издательство | Учитель, 2023 |
| Серия | Поурочное планирование для начальной школы |
| Электронная версия | скачать |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
1. Петерсон, Л. Г. Математика. 3 класс: в 3 частях. - М.: Ювента, 2012;
2. Петерсон, Л. Г. Математика. 4 класс: в 3 частях. - М.: Ювента, 2012.
В предлагаемом компакт-диске преподаватель сможет найти все необходимое для квалифицированной подготовки и качественного проведения уроков математики в 3-4 классах.
Содержание каждого урока включает большой объем справочной и рекомендательной информации, а также дополнительный материал (игровые, занимательные и разноуровневые задания), который способствует познавательной активности младших школьников. Предлагаемые разработки позволят учителю построить урок с учетом новых технологий и современных требований, а также совершенствовать практические навыки и умения учащихся.
Пособие предназначается учителям начальных классов общеобразовательных школ, лицеев, гимназий, а также может быть полезно студентам педагогических учебных заведений.
С этим товаром покупают
Примеры документов
Урок 1. Повторение
Урок 1. Повторение
(по выбору учителя, например сложение и вычитание
двузначных и трехзначных чисел)
Цель: повторение приемов сложения и вычитания двузначных и трехзначных чисел, решение простых задач на сложение и вычитание.
Оборудование: карточки для работы в парах.
Ход урока
I. Закрепление навыков устных вычислений (устный счет).
II. Повторение приемов сложения и вычитания.
1. Запись сложения и вычитания двузначных и трехзначных чисел в столбик (запись на доске).
254 +28 437 +329 512 – 175
86 + 647 532 – 48 700 – 319
Ученики решают примеры на доске и в тетрадях.
2. Составить выражения и найти их значение:
1) Из суммы чисел 162 и 473 вычесть разность чисел 450 и 415.
(162 + 473) – (450 – 415)
2) К разности чисел 928 и 473 прибавить сумму чисел 320 и 25.
(928 – 473) + (320 + 25)
Учитель зачитывает задания, дети составляют выражения в тетрадях и на доске.

3. Продолжить числовой ряд:
а) 128, 136, 144, … б) 9, 16, 24, 33, 43 …
Задание записано на доске заранее.
4. Работа в парах.
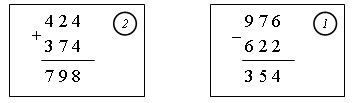
Дети получают карточки на сложение и вычитание трехзначных чисел.
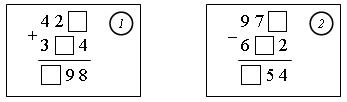
На обороте карточек записаны ответы напарника.
5. Найти задуманное число.

Ученики рассуждают: известна последовательность выполненных операций и полученный результат, поэтому для выполнения данного задания достаточно выполнить операции в обратном порядке.
316 + 204 – 73 – 347 = 100
х = 100

III. Решение простых задач.
Учитель зачитывает условие задачи, коллективно составляется схема.
В овощной ларек привезли 380 кг помидоров, 115 кг яблок, а груш столько, сколько помидоров и яблок вместе. Сколько всего овощей и фруктов привезли в ларек?
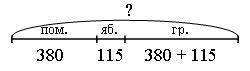
Ученики рассуждают: чтобы ответить на основной вопрос, необходимо найти количество привезенных груш. Для этого надо сложить число привезенных помидоров и яблок. Узнав количество груш, производим сложение.
380 + 115 + (380 + 115)
IV. Итог урока.
– Что повторяли на уроке?
– Что важно при сложении и вычитании чисел в столбик?
Задание на дом. Придумать по пять примеров на сложение и вычитание трехзначных чисел. Записать и решить столбиком.
Урок 2. Повторение
(по выбору учителя, например порядок действия
в выражениях; сочетательное свойство сложения,
понятия прямоугольника и квадрата)
Цель: повторение правил порядка действий в выражениях, сочетательного свойства сложения; повторение понятий прямоугольника и квадрата, вычисление их периметров.
Оборудование: чертежи прямоугольника и квадрата, карточки для работы в парах.
Ход урока
I. Закрепление навыков устных вычислений (устный счет).
II. Повторение правил порядка действий в выражениях.
Ученики вспоминают понятие «алгоритм» – порядок выполняемых действий по заданной программе.
1. Определить порядок действий в выражениях (записаны заранее на доске):
3 1 4 2 4 1 2 3
а) m + (n – a) – (d + c); в) m + (n – a – d + c);
3 1 2 4 1 2 4 3
б) m + (n – a – d) + c; г) (m + n – a) – (d + c).
2. Составить программу действий и выполнить:
1 5 2 3 6 4
а) (662 – 118) + (132 – 67 + 213) – (222 – 218);
4 1 5 2 3 6
б) 662 – (118 +132) + (67 + 213 – 222) – 218.
– Что вы заметили при решении этих примеров?

III. Повторение сочетательного свойства сложения.
1. Учащиеся вспоминают правило сочетательного свойства сложения на предложенных схемах.

Дети отмечают, что в обоих случаях значение выражения равно k, значит:
(a + b) + c = k a + (b + c) = k
(a + b) + c = a + (b + c)
2. Использование сочетательного свойства для рационализации вычислений:
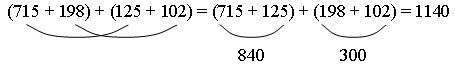
3. Самостоятельная работа с проверкой в классе.
(542 + 189) + 11; (742);
18 + (282 + 80); (380);
136 + 27 + 64 + 173; (400).

IV. Повторение понятий прямоугольника и квадрата, вычисление их периметров.
1. Учащиеся вспоминают, что в прямоугольнике противоположные стороны попарно равны, а у квадрата все стороны равны. Обратить внимание учеников на то, что в обеих фигурах все четыре угла – прямые.
На доске заранее начерчены прямоугольник и квадрат.
Дети предлагают различные значения длин сторон фигур.
Делается вывод:
Чтобы найти периметр этих фигур, необходимо сложить значения длин всех сторон. Можно выполнить вычисления другим способом: так как в прямоугольнике стороны попарно равны, достаточно сложить значения длин двух сторон (длины и ширины) и умножить на 2. В квадрате все стороны равны, поэтому достаточно значение длины одной стороны умножить на 4.
2. Практическая работа.
Учащиеся самостоятельно выбирают значения длин сторон и вычисляют периметр прямоугольника и квадрата.
3. Работа в парах.
Учащиеся получают карточки с чертежами фигур с указанием значений длин сторон. Необходимо вычислить периметр.
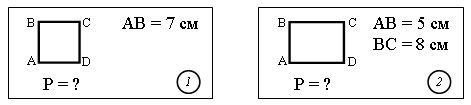
На обороте карточек записаны ответы напарника.
V. Итог урока.
– Что повторяли на уроке?
– Как можно использовать сочетательное свойство сложения?
– В чем схожесть и различие прямоугольника и квадрата?
Задание на дом.
Урок 3. Повторение
(по выбору учителя, например площадь прямоугольника;
таблица умножения, решение примеров на все случаи табличного
умножения и деления)
Цель: повторение и закрепление навыков решения примеров на все случаи табличного умножения и деления; нахождение площади прямоугольника.
Оборудование: плакаты с изображением прямоугольников.
Ход урока
I. Закрепление навыков устных вычислений (устный счет).
II. Нахождение площади прямоугольника.
1. Объяснение учителя.
– Площадь – это величина, определяющая, какое место фигура занимает на плоскости. Для измерения площади фигуры необходимо выбрать единицу измерения и определить, сколько раз она содержится в данной фигуре. Чаще всего при измерении площадей в качестве меры используют квадраты. В качестве общепринятых единиц измерения площадей выбирают квадрат со сторонами 1 см, 1 дм, 1 м. Эти единицы измерения называют квадратным сантиметром (1 см2), квадратным дециметром (1 дм2), квадратным метром (1 м2).
Дети самостоятельно придумывают и рисуют в тетрадях фигуры одинаковой площади (количество клеток определяют сами), но разной формы.
Например:
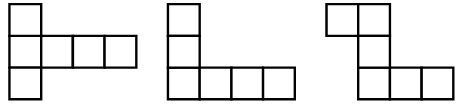
2. Самостоятельная работа. (Самопроверка в парах.)
На доске заранее начерчены прямоугольники или вывешены плакаты с изображением начерченных прямоугольников.
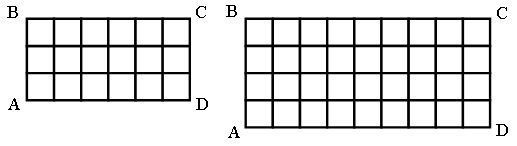
АВ = 3 см АВ = 4 см
вс = 6 см вс = 9 см
Найти площади прямоугольников (по клеточкам и в квадратных сантиметрах).

III. Повторение таблицы умножения. Решение примеров.
1. Вычислить:
24 : 6 · 3 20 : 5 · 4 18 : 6 · 5
3 · 9 : 3 64 : 8 · 5 54 : 9 · 6
27 : 9 · 4 40 : 5 · 3 81 : 9 · 4
2. Сравнить:
7 · 5 ![]() 5 · 6 8 · 6
5 · 6 8 · 6 ![]() 9 · 5
9 · 5
8 · 4 ![]() 6 · 7 3 · 7
6 · 7 3 · 7 ![]() 7 · 8
7 · 8
9 · 3 ![]() 3 · 8 4 · 6
3 · 8 4 · 6 ![]() 6 · 9
6 · 9

3. Найти значение выражений:
20 · 1 – 6 : 1 = ![]() 16 + 8 · 0 =
16 + 8 · 0 = ![]()
0 · 8 – 9 · 2 = ![]() (20 + 6) · 0 =
(20 + 6) · 0 = ![]()
15 : 1 + 18 : 18 = ![]() 40 · 1 – 50 · 0 =
40 · 1 – 50 · 0 = ![]()
4. Решить уравнения:
9 · х = 81 х : 9 = 5
48 : х = 8 х · 7 = 49
IV. Итог урока.
– Что повторяли на уроке?
– В каких единицах измеряется площадь?
– Как найти неизвестный множитель?
Задание на дом. Начертить прямоугольник со сторонами 2 см и 7 см. Найти его площадь.
Урок 4. Повторение
(по выбору учителя, например умножение и деление на 10 и 100;
объем фигуры; единицы объема)
Цель: повторение и закрепление приемов умножения и деления на 10 и 100, вычисления объема прямоугольного параллелепипеда, единиц объема: 1 см3, 1 дм3, 1 м3.
Оборудование: модель прямоугольного параллелепипеда, карточки для работы в парах, кубики.
Ход урока
I. Закрепление навыков устных вычислений (устный счет).
II. Повторение правил умножения и деления на 10 и 100.
Дети вспоминают, что при умножении на 10 и 100 к числу справа соответственно приписываются один или два нуля. А при делении – один или два нуля справа отбрасываются.
1. Выполнить деление:
60 : 10 = ![]() 440 : 10 =
440 : 10 = ![]() 200 : 10 =
200 : 10 = ![]()
30 : 10 = ![]() 500 : 100 =
500 : 100 = ![]() 900 : 100 =
900 : 100 = ![]()
2. Выполнить умножение:
8 · 10 = ![]() 55 · 10 =
55 · 10 = ![]() 2 · 100 =
2 · 100 = ![]()
10 · 3 = ![]() 10 · 4 =
10 · 4 = ![]() 100 · 12 =
100 · 12 = ![]()

3. Решить уравнения (работа в парах).

На обороте карточек записаны ответы напарника.
4. Выполнить обратные операции цепочки и заполнить пустые клетки (цепочка записана на доске):


III. Вычисление объема прямоугольного параллелепипеда. Единицы объема.
1. Дети рассматривают модель прямоугольного параллелепипеда.
Делается вывод:
Параллелепипед имеет грани, ребра, вершины.
Учитель задает вопросы:
– Сколько параллелепипед имеет граней (6), сколько ребер (12), сколько вершин (8)?
– Есть ли у него равные грани? (Нижняя и верхняя, передняя и задняя, правая и левая).
Выясняется, что противоположные грани фигуры равны.
Дети находят на модели параллелепипеда равные ребра и неравные ребра.
Вывод:
У параллелепипеда 3 неравных ребра: длина, ширина и высота.
Учитель напоминает, что длина, ширина и высота называются измерениями параллелепипеда, а нижняя грань – основанием.
2. Учитель составляет из кубиков модель параллелепипеда. Просит учащихся сосчитать, из скольких кубиков состоят длина, ширина и высота.
(Например: 4; 2; 2.)
– Как определить объем параллелепипеда, не пересчитывая кубики?
Дети сначала определяют количество кубиков в основании
(4 · 2 = 8), а затем оно умножается на число слоев (8 · 2 = 16).
3. Самостоятельная работа (самопроверка в парах).
Дети выбирают измерения в сантиметрах и находят объем параллелепипеда.
4. Творческая работа (работа в группах):
1-й ряд получает коробочку из-под гуаши;
2-й ряд – коробочку из-под скрепок;
3-й ряд – коробочку из-под спичек.
Задание: произвести измерения и вычислить объем фигуры (коллективная проверка).
IV. Итог урока.
– Что повторяли на уроке?
– Расскажите об особенностях умножения и деления на 10 и 100.
– Как вычислить объем параллелепипеда?
Урок 5. Повторение
(по выбору учителя, например свойства умножения;
деление с остатком)
Цель: повторение и закрепление свойств умножения, умения использовать их в вычислениях, производить деление с остатком.
Оборудование: таблицы свойств умножения.
Ход урока
I. Закрепление навыков устных вычислений (устный счет).
II. Арифметический диктант.
Найти:
– произведение чисел: 7 · 8; 5 · 4; 8 · 8; 3 · 7; 9 · 6;
– частное чисел: 27 : 9; 50 : 10; 48 : 6; 400 : 100; 8 : 8.
III. Повторение свойств умножения (переместительного и сочетательного).
Дети вспоминают о переместительном и сочетательном свойствах умножения.
a · b = b · a (a · b) · c = a · (b · c)
Делают вывод:
Значение произведения не зависит от порядка множителей и порядка действий. Это позволяет упрощать вычисления.
1. Вычислить, используя свойства умножения:
2 · 36 · 5 2 · 8 · 5 · 9 15 · 6
52 · 5 · 2 7 · 5 · 3 · 2 23 · 4
2 · 45 · 5 4 · 2 · 6 · 5 14 · 5
2. Составить и решить уравнения:
а) Какое число нужно вычесть из 526, чтобы получить 65?
б) Какое число нужно прибавить к 137, чтобы получить 485?
в) Из какого числа надо вычесть 314, чтобы получить 501?

3. Найти закономерность и продолжить ряд:
а) 565; 576; 587, … ; б) 999, 967, 935, … .
Составить программу действий и решить:
40 : (50 : 5) + 8 · (15 – 3 · 4) – 5 · 4.
4. Сравнить выражения:
5 · a ![]() a · 9 250 – d
a · 9 250 – d ![]() 25 – d
25 – d
c : 27 ![]() c : 72 n · 2 + n · 8
c : 72 n · 2 + n · 8 ![]() n · 10
n · 10
b – 13 ![]() b – 130 m + 140
b – 130 m + 140 ![]() m + 14
m + 14

IV. Деление с остатком.
Учитель просит пятерых учеников выйти к доске, а еще одному ученику дает 15 тетрадей и просит по одной тетради раздавать стоящим детям.
– Все ли тетради розданы? (Да.)
– Сколько тетрадей досталось каждому ученику? (3.)
Запишите выражение и решите его:
15 : 5 = 3.
Теперь учитель просит вернуть тетради раздававшему и добавляет еще 2 тетради. Действие возобновляется. Остались ли тетради после раздачи? (Да.) Сколько? (2.) Итак, 17 тетрадей нельзя поровну поделить между пятью учениками. Остается 2 тетради.
Запишем выражение и решим его.
17 : 5 = 3 (остаток 2), сделаем проверку:
3 · 5 + 2 = 17.
Вывод: Остаток всегда меньше делителя.
1. Выполнить деление и сделать проверку:
18 : 5 = 25 : 8 =
19 : 3 = 33 : 4 =
22 : 7 = 45 : 6 =
2. Решить уравнение и сделать проверку:
х · 8 = 640 х : 70 = 6
350 : х = 7 70 · х = 270
V. Итог урока.
– Что повторяли на уроке?
– Какие знаете свойства умножения?
– Каким должен быть остаток по отношению к делителю?
Задание на дом. Придумать и решить 6 примеров на деление с остатком. Сделать проверку.
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом








