Математика. 5-9 классы. Сценарии для предметной недели. Внеклассные мероприятия. Программа для установки через Интернет
| Код | СИ-5432 |
| Авторы-составители | Панишева О. В. |
| Издательство | Учитель, 2025 |
| Серия | ФГОС. Внеурочная деятельность |
| Электронная версия | скачать |
| УДК | 372.016:51*05/09 |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
Предназначено учителям математики, руководителям методических объединений, классным руководителям, студентам педагогических вузов.
Минимальные системные требования:
- операционная система - Windows XP/VISTA/7/8/8.1;
- процессор - Pentium-II;
- оперативная память - 256 МВ;
- разрешение экрана - 1024х768;
- свободное место на жестком диске - 400 МВ.
С этим товаром покупают
Примеры документов
Предисловие
Любить математику может не каждый,
Бывает, не каждый ее и поймет,
Но искорка пламени вспыхнет однажды
И пламень любви к ней в душе разожжет.
О. Панишева
Любовь к математике может быть врожденной и приобретенной. Время приобретения ее у каждого свое. У некоторых школьников любовь к математике возникает во время проведения и подготовки внеклассного мероприятия по предмету. Математический вечер, в какой бы форме он ни проводился, – это всегда праздник с присущими ему атрибутами: длительной подготовкой, репетициями, украшением зала, нарядами, музыкой, яркими впечатлениями. Приятные ощущения, вызванные внеклассным мероприятием, могут быть кратковременными и исчезнуть со словами ведущего: «Наш вечер окончен, спасибо за внимание», а могут, подпитываясь все новыми эмоциями от общения с математикой на уроке, перерасти в настоящую привязанность к царице наук. Немаловажным фактором является необычность происходящего на сцене и в зрительном зале на внеклассном мероприятии. Поэтому учителя стараются изобретать все новые и новые формы проведения математического праздника в рамках предметной недели. Внеклассные мероприятия всегда более эмоциональны, чем уроки, а положительные эмоции способствуют более долговременному сохранению полученной на празднике информации в памяти школьника.
Как считает Н. И. Кованцов, «любовь к математике станет еще большей, когда увидишь не только саму науку, а и тех неисчислимых подвижников, которые, не щадя усилий, целиком отдали себя великому делу служения математике и, как яркие факелы, освещали в ней дорогу далеко вперед». Именно поэтому практически не встретишь внеклассного мероприятия, где бы не присутствовали элементы истории математики, что позволяет подавать обучающимся не безымянную и безликую науку или просто фамилии, а конкретных людей с их позитивными и негативными чертами характера, личностей, у которых можно учиться, с которых следует брать пример. В период, когда ребенок ищет себя в этом мире, ему очень важно иметь пример для подражания; не исключено, что этим примером может стать один из выдающихся математиков.
Важнейшей задачей современной системы образования является формирование совокупности «универсальных учебных действий», обеспечивающих компетенцию «научить учиться», а не только освоение обучающимися конкретных предметных знаний и навыков в рамках отдельных дисциплин*. Формирование УУД происходит не только в учебной деятельности, но и во внеклассной работе по математике. Одним из средств формирования УУД являются игры и соревнования, которые неизменно присутствуют на математическом празднике. Участие во внеклассном мероприятии и победа в организованном соревновании могут служить косвенным и тем не менее объективным свидетельством сформированности УУД школьников.
Игровая деятельность всегда положительно эмоционально окрашена, потому является незаменимой в формировании личностных универсальных учебных действий: развитии интереса, мотивации, желания выполнять учебные действия; использовании фантазии, воображения при выполнении заданий. Игра может стать способом самосовершенствования, преодоления внутреннего конфликта, повышения настроения, активной мобилизации обучающихся. Любая игра является способом развития внимания, наблюдательности, сообразительности, сосредоточенности.
Подготовка и участие в играх и соревнованиях по математике способствуют и формированию познавательных учебных действий: поиск и выделение необходимой информации; применение методов информационного поиска, в том числе с помощью компьютерных средств. Участие в математических состязаниях предполагает наличие у обучающихся умений осуществлять для решения учебных задач операции анализа, синтеза, сравнения, классификации; устанавливать причинно-следственные связи; делать обобщения, выводы. Различные по формулировке игровые задания привлекают школьников к разным видам деятельности, формируя тем самым умение действовать в соответствии с поставленной целью.
Некоторые исследователи считают игру формой общения учеников. Действительно, вне контактов, взаимодействия, взаимопонимания между участниками никакой игры быть не может. Игра предполагает общение обучающихся между собой и с учителем, что способствует формированию коммуникативных учебных действий. Если дети знают, что им предстоит участвовать в командных соревнованиях, то более ответственно относятся к подготовке к такой игре, чтобы не подвести товарищей.
В пособии представлены сценарии авторских внеклассных мероприятий, проводимых в разные годы. Книга поможет учителю сэкономить время при подготовке к празднику. Преподаватель может использовать только часть сценария, понравившуюся ему форму организации праздника, определенную игру, наполнив ее новым содержанием. Надеемся, что данные сценарии помогут высечь ту искорку любви к математике, из которой в дальнейшем разгорится настоящая любовь к ней!
Литература
1. Арнаудов, Д. Декартовы координаты / Д. Арнаудов // Позакласний час. – 1997. – № 4. – С. 29.
2. Болховитинов, В. Н. Твое свободное время. Занимательные задачи, опыты, игры / В. Н. Болховитинов, Б. И. Колтовой, И. К. Лаговский. – М. : Детская литература, 1975.
3. Василенко, О. О. Серенада математиці / О. О. Василенко. – Харків : Вид. гр. «Основа», 2003.
4. Василенко, О. О. Серенада математиці / О. О. Василенко. – Харкiв : Вид. гр. «Основа», 2009.
5. Волкова, Т. Н. 1000. Творческие игры, задания и тесты для развития памяти и внимания у детей 6–12 лет / Т. Н. Волкова. – Донецк : ООО ПКФ «БАО», 2005.
6. Галай, Г. І. Учням про видатних математиків / Г. І. Галай, Г. Д. Гриневич. – Київ : Радянська школа, 1976.
7. Демьянов, В. П. Геометрия и Марсельеза / В. П. Демьянов. – М. : Знание, 1979.
8. Депман, И. Я. За страницами учебника математики / И. Я. Депман, Н. Я. Виленкин. – М. : Просвещение, 1989.
9. Кун, Н. А. Легенды и мифы Древней Греции / Н. А. Кун. – Ростов н/Д : Феникс, 1998.
10. Лиман, М. М. Школьникам о математике и математиках / М. М. Лиман. – М. : Просвещение, 1981.
11. Математика в афоризмах, цитатах, высказываниях / сост. Н. А. Вирченко. – Київ : Вища школа, 1983.
12. Математика в стихах : задачи, сказки, рифмованные правила. 5–11 классы / авт.-сост. О. В. Панишева. – Волгоград : Учитель, 2009.
13. Математика. Дитяча енциклопедія. – Харків : Фоліо, 2003.
14. Математична хрестоматія / под ред. М. І. Кованцова. – Київ: Радянська школа, 1977.
15. Михеева, Т. Н. Софизмы. Алгебра. Геометрия. Тригонометрия : пособие для учащихся и учителей средней школы / Т. Н. Михеева. – М. : Грамотей, 2007.
16. Панишева, О. В. Математика в стихах : задачи, сказки, рифмованные правила. 5–11 классы / О. В. Панишева. – Волгоград : Учитель, 2009.
17. Панішева, О. В. Граймо з математикою / О. В. Панішева. – Харкiв : Вид. гр. «Основа», 2013.
18. Селищев, Е. Н. География для любознательных, или О чем не узнаешь на уроке / Е. Н. Селищев. – Ярославль : Академия развития : Академия Холдинг, 2002.
19. Шмигевський, М. В. Видатні математики / М. В. Шмигевський. – Харків : Вид. гр. «Основа», 2004.
20. Энциклопедия для детей. Т. 11. Математика / гл. ред. М. Аксенова. – М. : Аванта +, 2004.
21. Я познаю мир. Математика : дет. энциклопедия. – М. : АСТ : Астрель, 2004.
Путешествие в город Математических загадок (для обучающихся 5–7 классов)
Путешествие
в город математических загадок
(для обучающихся 5–7 классов)
Класс поделен на две команды.
Ведущий. Сегодня мы совершим путешествие в город Математических загадок.
Конкурс 1.
Эта история началась с того, что у всех детей пропали их любимые игрушки: компьютеры, приставки, плееры, куклы, собачки, шоколадки – все, что они любили, с чем проводили свободное время, приходя из школы домой. Это двойки, которые поселились у детей в тетрадках, увели игрушки в город Математических загадок. А найти игрушки сможет лишь тот, кто дружит с математикой. (На сцену приглашаются заранее выбранные две команды.)
Не забудьте взять с собой в дорогу дружбу, находчивость, смекалку и хорошее настроение. Все собрали? Кажется, хорошего настроения маловато. Чтобы его прибавилось, каждая команда должна спеть песню, в которой есть цифры, – это и будет первым вашим испытанием.
Конкурс 2.
Ведущий. Спев песню, команды отправляются в путь и оказываются у высоких красивых ворот, преграждающих путь в волшебный город. Ворота закрыты на 3 замка. Расшифровав секрет каждого замка, вы сможете его открыть (демонстрирует плакаты, дает задание найти закономерность).
1) 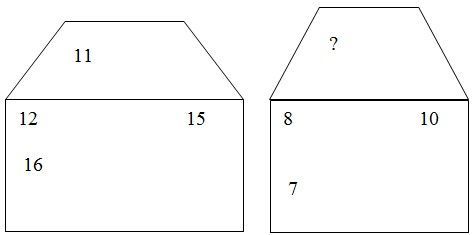
Ответ: 11 (12 + 15 = 27 и 11 + 16 = 27; 8 + 10 = 18, 7 + + … = = 18).
29, ? , 56.
Ответ: 27 (16 + 27 = 43, 29 + … = 56).
Ответ: 16 (квадраты натуральных чисел).
Пока команды размышляют, для зрителей проводится мини-аукцион: «Знаете ли вы ученых-математиков?». Выигрывает тот, кто назовет последнего.
Ведущий. Итак, команды справились с заданием – ворота распахнулись, и вы оказались в городе Математических загадок. В городе много улиц. По каждой из них предстоит пройти, чтобы отыскать улицу Двоек.
Первая улица – улица Математических терминов. В каждом доме хранятся предметы, связанные с математикой, начинающиеся на одну и ту же букву. Например, в доме № 2 находятся предметы, начинающиеся на вторую букву алфавита – «Б»: биссектриса, бином, боковые стороны и пр.
Конкурс 3.
Ведущий. Я называю букву, а команды должны вспомнить математические термины на эту букву. На обдумывание дается 5 секунд. Если вариантов нет, ходит другая команда.
Вы удачно пересекли улицу Математических терминов и оказались на площади Задач. Здесь хранятся те задачи, которые ученики решают на уроках. Задачи, которые вы решили правильно, отдыхают, а те, которые недорешали, так и бросаются на каждого встречного и просят: «Реши меня!»
Конкурс 4.
Команды решают задачи по теме, изучаемой в данный момент на уроках (записаны на листочках).
Ведущий. А в это время мы проверим, как умеют решать задачи наши зрители.
Задача 1.
Сидят рыбаки, стерегут поплавки.
Рыбак Корней поймал 13 окуней,
Рыбак Евсей – четырех карасей,
А рыбак Михаил двух сомов изловил.
Сколько рыб рыбаки
Натаскали из реки? (19.)
Задача 2.
Вы летите в самолете,
Вы летите, вы поете.
С облаков спустились в класс.
Вдруг учитель спросит вас:
«От Москвы до Ленинграда
В 3 часа добраться надо.
В час бензина выгорать
Будет литров 25.
Двенадцать (внеклассное межпредметное мероприятие для обучающихся 6 классов)
Двенадцать
(внеклассное межпредметное мероприятие
для обучающихся 6 классов)
Ход мероприятия
Ведущий 1. Здравствуйте, уважаемые участники и болельщики. Мы рады приветствовать вас на математическом празднике, который носит лаконичное и необычное название – «Двенадцать». Это название выбрано не случайно. Число 12 очень часто используется в нашей жизни и имеет непосредственное отношение именно к шестиклассникам, большинству из которых 12 лет. Уважаемые болельщики, ну-ка ответьте, что у вас ассоциируется с числом 12? (12 месяцев в году; 12 зодиакальных созвездий; 12 цифр на циферблате часов; 12 подвигов Геракла; 12 апостолов; поэма А. Блока «Двенадцать»; сказка «Двенадцать месяцев» и т. д.)
Ведущий 2. Число 12 почиталось у многих народов. Число, следующее за ним, казалось чем-то излишним, чрезмерным. У шумеров несчастливым считался 13-й месяц, который они время от времени вставляли в свой календарь, чтобы согласовать лунные месяцы с солнечным годом. Отсюда, вероятно, и пошел предрассудок о том, что число 13 несчастливое. В некоторых западных странах до сих пор не ходят 13-е номера трамваев, в небоскребах нет 13-го этажа и действуют фирмы, в которых можно пригласить к праздничному ужину 14-го гостя, если вдруг за столом собралось 13 человек.
Ведущий 1. Но мы не верим в приметы, и все числа для нас одинаково хороши. Сегодня уделим более пристальное внимание числу 12. Почему? Потому что в 6 классе большинству из вас исполняется именно 12 лет. В конкурсе принимают участие 12 человек, 2 команды (команда мальчиков и команда девочек) в составе 5 игроков и капитана, которые были выбраны заранее. 12 заданий придется выполнить сегодня игрокам, и каждое из них связано с числом 12. И наконец, 12 баллов получит каждый игрок выигравшей команды.
Задание 1. Сегодня мы с вами, как и большинство учеников из других стран мира, пользуемся десятичной системой счисления, то есть считаем десятками, сотнями, тысячами и другими степенями числа 10. Но было время, когда серьезным соперником десятичной системы счисления была двенадцатеричная, в которой вместо десятков применяли при счете дюжины, то есть группы из 12 предметов. Именно с этим словом связано слово «недюжинный» – не похожий на остальных. А в торговле применяли и дюжину дюжин, которую называли «большой дюжиной», или «гроссом». Так что, пересчитав предметы в двенадцатеричной системе счисления, можно было сказать: 5 гроссов, 8 дюжин и еще 6 предметов. Несколько раз совершались попытки ввести двенадцатеричную систему, то есть вместо десятков и сотен считать дюжинами и гроссами; в частности, пытался это сделать шведский король Карл ХІІ, разгромленный русскими войсками под Полтавой.
Ведущий 1. При выполнении первого задания вы сможете почувствовать, как бы считалось нам, если бы идеи Карла ХІІ увенчались успехом. Вроде бы ничего особенного: ведь до сих пор некоторые товары – вилки, ложки, ножи – продают дюжинами, а в столовые сервизы входят по 12 разных тарелок и блюдец.
Ведущий 2. Итак, задание: выслушав стихотворение, подсчитать в двенадцатеричной системе счисления количество предметов, упоминаемых в нем, то есть дать ответ в гроссах и дюжинах. (Чтение стихотворения может сопровождаться инсценировкой сервировки праздничного стола.)
Решила Таня окунуться в древность,
На стол поставила 3 дюжины тарелок:
Глубоких, мелких, маленьких совсем,
Пересчитала, чтоб гостям хватило всем.
У Тани ведь сегодня званый ужин!
Достала девочка еще и чашек дюжину,
12 блюдец приготовила для торта,
По дюжине ножей и вилок для комфорта.
12 ложек оказалось на столе
И дюжина стаканов для компота.
И, оглядев подружек во дворе,
Вздохнула: «Праздники – одна забота».
12 лет сегодня Тане исполняется,
Стол накрывает девочка, старается.
На стол добавила 3 дюжины салфеток
И вазу с шоколадными конфетами.
Еще графин поставила с компотом,
12 свечек к праздничному торту.
И вот, добавив вазочку с вареньем,
Стол оглядела с удовлетвореньем.
Успела сосчитать она при этом
Количество всех на столе предметов.
Я нынче вам задам вопрос простой:
Предметов сколько принесла она на стол?
Я люблю математику (внеклассное мероприятие для обучающихся 7 классов)
Я люблю математику
(внеклассное мероприятие для обучающихся 7 классов)
В конкурсе принимает участие 2 команды (команда мальчиков и команда девочек) в составе 4 игроков и капитана, которые выбираются заранее. Каждый игрок имеет свой номер. Все присутствующие в зале делятся на зрителей и болельщиков. У каждой команды свои болельщики. Они имеют знаки отличия (эмблему, ленточку, флажки) в соответствии с тем, за какую команду болеют. Располагаются в зале компактно, с той стороны, где находится их команда.
Игра состоит из двух этапов: личных соревнований участников и коллективных. Баллы за те и другие начисляются всей команде. На первом этапе сначала соревнуются первые номера команд, потом вторые и т. д. Если игрок не ответил, то на этот вопрос может дать ответ игрок с тем же номером из другой команды. На втором этапе игры болельщики могут подсказывать своей команде, если она затрудняется с ответом.
Ход мероприятия
Ведущие. Только любить – и никак иначе,
Только любить – такова задача.
С ней в ногу идти, в унисон дышать,
С новых сторон ее открывать.
Лишь тот математик, кто думать умеет,
Лишь тот математик, в ком сомнений есть семя,
Кто то замечает, что не видит другой,
Кто проявляет к науке любовь.
1-й этап.
Конкурс 1 «Музыкальный» (для первых номеров команд). Послушайте минусовки песен, запишите числа, которые в ней упоминаются. Затем необходимо найти сумму записанных чисел. Кто сделает это точнее и быстрее? Если оба игрока ошиблись, побеждает тот, чей ответ ближе к правильному.
Например:
«Двести лет» (муз. В. Малежика, сл. П. Хмара-Миронова);
«Через две зимы» (муз. В. Шаинского, сл. М. Пляцковского);
«Жили у бабуси два веселых гуся» (песня из мультфильма «Два веселых гуся», «Союзмультфильм», 1970 г.);
«33 коровы» (муз. М. Дунаевского, сл. Н. Олева);
«Миллион алых роз» (муз. Р. Паулса, сл. А. Вознесенского) и т. д.
Конкурс 2 «Объяснялки». Вторые номера команд получают от ведущего лист с написанными на нем 10 математическими терминами или именами ученых-математиков. Участники должны объяснить эти термины, не называя их прямо. Сколько терминов угадает команда, столько баллов она получит. Время на отгадывание с объяснением – 2 мин.
Для первой команды: гипотенуза, Пифагор, плюс, неравенство, корень, цифра, квадрат, алгебра, циркуль, аксиома.
Для второй команды: периметр, Гаусс, равенство, миллион, треугольник, угол, дробь, геометрия, скобки, число пи.
Конкурс 3 «Кинокритик». Показывается кинофрагмент (или зачитывается отрывок из литературного произведения, где есть сюжет, связанный с математикой). Задание – назвать произведение (кинофильм).
Например:
Фильм-сказка «Двенадцать месяцев» (реж. А. Грапик, «Ленфильм», 1972 г.) (фрагмент, в котором принцесса неправильно рассказывает таблицу умножения).
Мультфильм «Вовка в Тридевятом царстве» (реж. Б. Степанцев, «Союзмультфильм», 1965 г.) (фрагмент про слет Василис Премудрых).
Конкурс 4 «Переводчики». Ведущий говорит буквальное значение какого-либо математического термина, заимствованного из другого языка. Игрок должен назвать этот математический термин.
Для первой команды: этот термин в переводе с латинского означает «луч», «спица колеса». (Радиус.)
Для второй команды: это слово происходит от двух латинских слов, которые переводятся как «висеть» и «верх», то есть все слово переводится как «висящий сверху», или «отвесный». (Перпендикуляр.)
Конкурс 5 «Определенность». В математике есть много терминов, которые являются с точки зрения языка многозначными словами. Игрокам нужно из всех перечисленных математических терминов выбрать один, который не является многозначным.
Для первой команды: корень, шар, уравнение, функция.
Для второй команды: дробь, гипотенуза, вертикальный.
2-й этап.
Ответ дается после коллективного обсуждения командой в течение 20 с. Право выбора правильного ответа из всех звучащих в процессе обсуждения предоставляется капитану.
Конкурс 1 «Как правильно понять». Каждой команде дается 3 толкования некоторого факта. Задание – выбрать правильное.
Для первой команды: в древности «алгебраистами» называли:
1) костоправов;
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом












